
20. (本小题满分12分)
已知椭圆 的中心在坐标原点
的中心在坐标原点 ,一条准线的方程为
,一条准线的方程为 ,过椭圆的左焦点
,过椭圆的左焦点 ,且方向向量为
,且方向向量为 的直线
的直线 交椭圆于
交椭圆于 两点,
两点, 的中点为
的中点为
(1)求直线 的斜率(用
的斜率(用 、
、 表示);
表示);
(2)设直线 与
与 的夹角为
的夹角为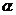 ,当
,当 时,求椭圆的方程.
时,求椭圆的方程.
19. (本小题满分12分)
如图所示,直三棱柱 中,
中,



 ,点
,点 在
在 上且
上且 =
=
(1)求证: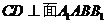 ;
;
(2)求二面角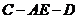 的大小.
的大小.
18.(本小题满分12分)
(理)2008年在中国北京成功举行了第29界奥运赛,其中乒乓球比赛实行五局三胜的规则,即先胜三局的获胜,比赛到此宣布结束。在赛前,有两个国家进行了友谊赛,比赛双方并没有全部投入主力,两队双方较强的队伍每局取胜的概率为0.6,若前四局出现2比2平局,较强队就更换主力,则其在决赛局中获胜的概率为0.7,设比赛结束时的局数为
(1) 求 的概率分布;
的概率分布;
(2) 求E .
.
(文)在“灿烂阳光小歌手PK赛”10进6的比赛中,有男歌手和女歌手各3人进入前6名,现从中任选2名歌手去参加2010年的元旦联欢会的演出,求:
(1) 恰有一名参赛歌手是男歌手的概率;
(2) 至少有一名参赛歌手是男歌手的概率;
(3) 至多有一名参赛歌手是男歌手的概率.
17.(本小题满分10分)
向量 ,设函数
,设函数
 为常数)
为常数)
(1) 若 为任意实数,求
为任意实数,求 的最小正周期;
的最小正周期;
(2) 若 在
在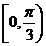 上的最大值与最小值之和为
上的最大值与最小值之和为 ,求
,求 的值.
的值.
16.具有性质 =
= 的函数,我们称其为满足“倒负”变换的函数,下列函数:
的函数,我们称其为满足“倒负”变换的函数,下列函数:
(1) =
= -
- ;(2)
;(2) =
= +
+ ;(3)
;(3) =
= ,其中不满足“倒负”变换的函数是 .
,其中不满足“倒负”变换的函数是 .
15.设 ,若非
,若非 是非
是非 的充分不必要条件,那么
的充分不必要条件,那么 是
是
 条件,
条件, 的取值范围是
的取值范围是
14.(理)在一次模拟考试中,由于试卷保存不利造成纸张破损,具体如下:在 中,已知
中,已知
 (纸张破损处),求角
(纸张破损处),求角 。并推断破损处的条件为三角形一边的长度,根据答案
。并推断破损处的条件为三角形一边的长度,根据答案 ,你能帮老师将条件补充完整吗?
,你能帮老师将条件补充完整吗?
(文)关于 的方程
的方程 有一根为
有一根为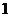 ,则
,则 是
是 三角形.
三角形.
13.(理)函数 在点
在点 处连续,则
处连续,则 的值是 .
的值是 .
(文)某连队身高符合建国60周年国庆阅兵标准的士兵共有45人,其中18岁-21岁的士兵有15人,22岁-25岁的士兵有20人,26岁-29岁的士兵有10人,若该连队有9个参加国庆阅兵的名额,如果按年龄分层选派士兵,那么,该连队年龄在26岁-29岁的士兵参加国庆阅兵的人数为 .
12.(理)将一颗骰子投掷两次,第一次出现的点数记为 ,第二次出现的点数记为
,第二次出现的点数记为 ,
,
设两条直线l1:ax+by=2,l2:x+2y=2平行的概率为P1,相交的概率为P2,试问点(P1,P2)与直线l2:x+2y=2的位置关系是
A.P在直线l2的右下方 B.P在l2直线的左下方
C.P在直线l2的右上方 D.P在直线l2上
(文)连掷两颗骰子得到的点数分别记为 和
和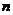 ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,则
,则 的概率是
的概率是
A. B.
B. C.
C. D.
D. 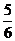
第Ⅱ卷(非选择题 共90分)
11.半径为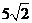 的球面上有三个点
的球面上有三个点 ,若
,若 ,经过这3个点作截面,那么球心到截面的距离为
,经过这3个点作截面,那么球心到截面的距离为
A.4
B. C.5
D.9
C.5
D.9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com