
2.3一法多解,渗透思想方法。
在习题教学中要改变传统的就题讲题现象,要使学生领会透过现象抓住事物的本质的方法,即抓住物理性质和物理过程,将复杂问题分解成若干简单问题,并抓住这几个简单问题之间的联系,找出其中的规律性,这是一个基本的物理思想方法。所以,习题教学要利用一法多解的形式,渗透科学的思想方法,使学生感悟如何处理问题和解决问题, 确定解题思路, 然后考虑运用相应的物理规律, 这将使学生的知识和能力达到一个新的水平,可提高习题教学的效益。
3 改进教法,提高效益
2.2一题多变,
调动思维按照由易到难、循序渐进的原则, 将基础题加以改造,围绕教材中的基础知识,恰当地引伸、扩展利变更, 让涉及到的有关知识“协调作战”,通过对原题的一次义一次的变化, 加深难度, 拓宽考杏范围, 贯穿知识点, 开阔思路, 举一反三。这样可调动学生的思维, 激发其兴趣, 培养他们的应变能力, 有助于学生将学过的知识融会贯通,提高习题教学的效益。
2.1 一题多解,培养学生的发散思维
物理现象的变化一般都有规律性,而这些规律是相互联系的, 因此, 一个物理问题往往是可以通过多种途径,用多种联系的方法去思考和寻求答案的。如果单纯用一种思维方式思考, 有时将陷入困境, 教师应指导学生善于从不同的角度,不同的方向去思考问题。利用一题多解的方式,能达到这一目的。所以, 加强一题多解训练,可巩固学生的知识基础, 发展学生的发散性思维,进一步对所学知识的理解和深化应用, 培养学生的创造能力,提高习题教学的效益。
8.解:设切点为 ,则切线方程为
,则切线方程为 ,
,
得切线与 轴分别交于
轴分别交于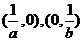 ,令
,令 ,
,
而点 在圆
在圆 上,则
上,则 ,
,
得 ,即面积的最小值为
,即面积的最小值为 ,且当
,且当 时,等号成立,
时,等号成立,
此时 ,则切线方程为
,则切线方程为 ,
, ,
,
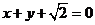 ,或
,或 .
.
8.求圆 的切线和两坐标轴围成的三角形的面积的最小值,并求取得最小值时
的切线和两坐标轴围成的三角形的面积的最小值,并求取得最小值时
切线的方程.
7.解:圆 关于直线
关于直线 对称的圆是:
对称的圆是:
圆 ,
,
整理得: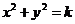 ,而该与圆直线
,而该与圆直线 相切,
相切,
则 ,得
,得 .
.
7.已知圆 关于直线
关于直线 对称的圆是
对称的圆是 ,且
,且 与
与
直线 相切,求实数
相切,求实数 的值.
的值.
6.解:圆 关于原点对称的圆的方程为
关于原点对称的圆的方程为
圆 ,整理得:
,整理得: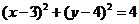 ,
,
因为两圆为等圆,所以这两个圆的两条外公切线均与连心线平行,
而两圆的连心线的斜率为 ,
,
设这两个圆的外公切线方程为 ,
,
得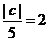 ,即
,即 ,
,
所以这两个圆的外公切线方程为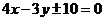 .
.
6.求圆 关于原点对称的圆的方程,并求这两个圆的外公切线方程.
关于原点对称的圆的方程,并求这两个圆的外公切线方程.
5.解:该切线的斜率显然存在,设 ,即
,即 ,
,
圆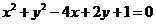 的标准方程为
的标准方程为 ,
,
则 ,
, ,得
,得 ,即
,即 ,
,
得切线方程为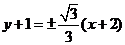 ,
,
即 ,或
,或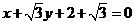 ;
;
设切点坐标为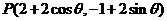 ,而
,而 ,
,
即 ,得
,得 ,
,
得切点坐标为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com