21．(本题满分13分)

已知数列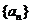的各项均是正数，其前n项和为，其中p为正常数，且，

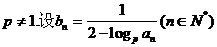　 (I)求数列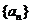的通项公式；

　 (II)设数列项和为，是否存在正整数m，使得对于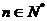恒成立，若存在，求出m的最小值，若不存在，说明理由；

　 (III)试证明：当

20．(本题满分13分)

已知椭圆的左、右焦点分别为F₁、F₂，短轴端点分别为A、B，且四边形F₁AF₂B是边长为2的正方形。

　 (I)求椭圆的方程；

　 (II)若C、D分别是椭圆长轴的左、右端点，动点M满足，连结CM交椭圆于P，证明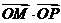为定值(O为坐标原点)；

　 (III)在(II)的条件下，试问在x轴上是否存在异于点C的定点Q，使以线段MP为直线的圆恒过直线DP、MQ的交点，若存在，求出Q的坐标，若不存在，说明理由。

19．(本题满分13分)

某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交a元()的管理费，预计当每件产品的售价为x元()时，一年的销售量为万件．

　 (1)求分公司一年的利润(万元)与每件产品的售价的函数关系式；

　 (2)当每件产品的售价为多少元时，分公司一年的利润最大，并求出的最大值．

18．(本题满分12分)

　　　　 已知等腰梯形PDCB中(如图1)，PB=3，DC=1，PD=BC=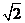，A为PB边上一点，且PA=1，将△PAD沿AD折起， 使面PAD⊥面ABCD.

　 (I)证明：平面PAD⊥平面PCD；　

　 (II)试在棱PB上确定一点M，使截面AMC把该几何体分成的两部分PDCMA与MACB的体积的比为2：1；

　 　 (III)在M满足(II)的情况下，求二面角M-AC-P的余弦值。

17．(本题满分12分)

有编号为1，2，3，…，n的n个学生，入坐编号为1，2，3，…，n的n个座位。每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为，已知时，共有6种坐法．

(Ⅰ)求n的值；

(Ⅱ)求随机变量的概率分布列和数学期望．

16．(本题满分12分)

　　 已知点，O为坐标原点。

　 (I)若的值；

　 (II)若实数m，n满足的最大值。

15．给出定义：若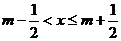(其中m为整数)，则m叫做离实数x最近的整数，记作{x}，即，在此基础上给出下列关于函数的四个命题：

　　　　 ①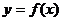的定义域是R，值域是；

　　　　 ②点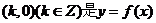的图像的对称中心；

　　　　 ③函数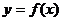的最小正周期为1；

　　　　 ④函数上是增函数；

　　 则其中真命题是　　　　　 。

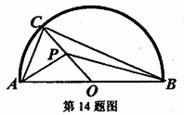
14．如图，半圆的直径AB=6，O为圆心，C为半圆上不同于

A、B的任意一点，若P为半径OC上的动点，则

的最小值是　　　　 。

13．当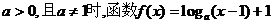的图像恒过点A，若点A在直线

　 的最小值为　　　　　 。