2．下列化学用语正确的是

A．乙烯的结构简式　 CH₂CH₂

B．氧化钠的电子式　

C．明矾的化学式　　 KAISO₄·12H₂O

D．乙酸乙酯的分子式　 C₄H₈O₂

1．下列有关金属的说法中，不正确的是

A．青铜、不锈钢、赢铝都是合金

B．铜表面易形成致密的氧化膜

C．工业上用电解熔融MgCl_2­的方法制取金属镁

D．铝是活泼金属，但在空气中耐腐蚀

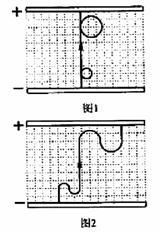
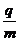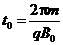2．(带电粒子在电场中的运动+带电粒子在磁场中的运动)两块足够大的平行金属极板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向)．在t＝0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力)．若电场强度E₀、磁感应强度B₀、粒子的比荷均已知，且，两板间距．

⑴求粒子在0-t₀时间内的位移大小与极板间距h的比值；

⑵求粒子在板板间做圆周运动的最大半径(用h表示)；

⑶若板间电场强度E随时间的变化仍如图1所示，磁场的变化改为如图3所示，试画出粒子在板间运动的轨迹图(不必写计算过程)．

解法一：⑴设粒子在0-t₀时间内运动的位移大小为s₁

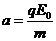
又已知

解得：　

⑵粒子在t₀-2t₀时间内只受洛伦兹力作用，且速度与磁场方向垂直，所以粒子做匀速圆周运动．设运动速度大小为v₁，轨道半径为R₁，周期为T，则

解得：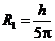

又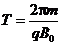 　　　　　

即粒子在t₀-2t₀时间内恰好完成一个周期的圆周运动．在2t₀-3t₀时间内，粒子做初速度为 v₁的匀加速直线运动，设位移大小为s₂

解得：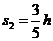　　　

由于s₁+s₂＜h，所以粒子在3t₀-4t₀时间内继续做匀速圆周运动设速度大小为v₂，半径为R₂

解得：

由于s₁+s₂+R₂＜h，粒子恰好又完成一个周期的圆周运动．在4t₀-5t₀时间内，粒子运动到正极板(如图1所示)．因此粒子运动的最大半径

⑶粒子在板间运动的轨迹如图2所示

解法二：由题意可知，电磁场的周期为2t₀，前半周期粒子受电场作用做匀加速直线运动，加速度大小为

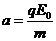　　　 　　　　　　　　　　　　方向向上

后半周期粒子受磁场作用做匀速圆周运动，周期为T

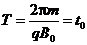
粒子恰好完成一次匀速圆周运动．至第n个周期末，粒子位移大小为s_n

又已知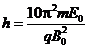　 　

由以上各式得：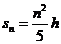

粒子速度大小为：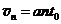

粒子做圆周运动的半径为：

解得：

显然：s₂+R₂＜h＜s₃

⑴粒子在0-t₀时间内的位移大小与极板间距h的比值　

⑵粒子在极板间做圆周运动的最大半径　 　

⑶粒子在板间运动的轨迹图见解法一中的图2

1.(带电粒子在磁场中的运动+周期性)空间存在垂直于纸面方向的均匀磁场其方向随时间作周期性变化，磁感应强度B随时间变化的图线如图(甲)所示。规定B>0，时，磁场方向穿出纸面。现在磁场区域中建立一与磁场方向垂直的平面直角坐标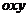，如图(乙)所示。一电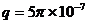量C质量kg的带正电粒子，位于原点O处，在时刻以初速度m/s沿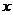轴正方向开始运动，不计重力作用，不计磁场变化可能产生的一切其他影响。求：

　 (1)带电粒子的运动半径；

　 (2)带电粒子从O点运动到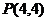点的最短时间；

　 (3)要使带电粒子过图中的点，则磁场的变化周期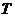为多少？

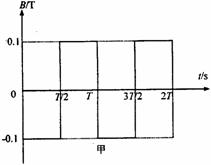
解：(1)设粒子运动半径为R，则

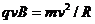　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

　　　　　　　　　 m　　　　　　　　　　　　　　　　　　　　　　　　　 2分

　 (2)设点电粒子的运动周期为，则

　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 1分

　　 若磁场的变化周期恰好为带电粒子运动的，即它的轨迹为4个1/4圆相连接，它的运动轨迹如图所示，此种情况带点粒子从O点运动到P点所用的时间最短，设为，则

　　　　 　　　3分

　 (3)要使带电粒子经过P点，则磁场变化的周期T和带电粒子在磁场中的运动周期之间应满足的关系为

　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

　　　 即　　　　 　　　　　　　 2分

6.初速度为零的离子经过电势差为U的电场加速后，从离子枪T中水平射出，与离子枪相距d 处有两平行金属板MN和PQ，整个空间存在一磁感强度为B的匀强磁场如图所示。不考虑重力的作用，荷质比q／m(q，m分别为离子的带电量与质量)，应在什么范围内，离子才能打到金属板上？

[错解]离子在离子枪内加速，出射速度为

由牛顿第二定律离子在磁场中离子的加速度为

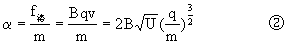
离子在磁场中做平抛运动

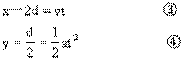
[错解原因]离子在离子枪中的的加速过程分析正确，离子进入磁场的过程分析错误。做平抛运动物体的加速度为一恒量，仅与初速度垂直。而洛伦兹力总与速度方向垂直，洛伦兹力大小不变、方向变化，它是个变力。离子在磁场中应做匀速圆周运动。

[分析解答]设离子带负电，若离子正好打到金属板的近侧边缘M，则其偏转半

若离子正好打到金属板的远侧边缘N，则其偏转半径满足关系

即

因离子从离子枪射出的速度v由离子枪内的加速电场决定

即

代入式④即得

讨论：由以上方程组可知

[评析]本题考查的能力要求体现在通过对边界条件的分析，将复杂的问题分解为若干个简单问题；把未知的问题转化为已知条件。并且通过几何关系找出大小两个半径来。从错解中还可以看出，熟练掌握基本的物理模型的特点(加速度与初速度的关系或加速度与位移之间的关系等)对正确选择解题思路的重要性。

5. 如图为方向相互垂直的匀强电场和匀强磁场区域。电场强度为E，磁感强度为B，复合场的水平宽度为d，竖直方向足够长。现有一束电量为+q、质量为m初速度各不相同的粒子沿电场方向进入场区，求能逸出场区的粒子的动能增量ΔE_k。

[错解]当这束初速度不同、电量为+q、质量为m的带电粒子流射入电场中，由于带电粒子在磁场中受到洛伦兹力是与粒子运动方向垂直的，粒子将发生不同程度的偏转。有些粒子虽发生偏转，但仍能从入射界面的对面逸出场区；有些粒子则留在场区内运动。

从粒子射入左边界到从右边界逸出，电场力做功使粒子的动能发生变化。根据动能定理有：

Eqd=ΔE_k

[错解原因]错解的答案不错，但是不全面。没有考虑仍从左边界逸出的情况。

[分析解答]由于带电粒子在磁场中受到洛伦兹力是与粒子运动方向垂直的。它只能使速度方向发生变。粒子速度越大，方向变化越快。因此当一束初速度不同、电量为+q、质量为m的带电粒子射入电场中，将发生不同程度的偏转。有些粒子虽发生偏转，但仍能从入射界面的对面逸出场区(同错解答案)；有些粒子将留在场区内运动；有些粒子将折回入射面并从入射面逸出场区。由于洛伦兹力不会使粒子速度大小发生变化，故逸出场区的粒子的动能增量等于电场力功。对于那些折回入射面的粒子电场力功为零，其动能不变，动能增量ΔE_k=0。

[评析]本题考查带电粒子在磁场中的运动和能量变化。这道题计算量很小，要求对动能定理、电场力、磁场力等基本概念、基本规律有比较深入的理解，而且能够与题目所给的带电粒子的运动相结合才能求得解答。在结合题意分析时，特别要注意对关键词语的分析。本题中：“逸出场区”的准确含义是从任何一个边界逸出场区均可。

4.一个负离子的质量为m，电量大小为q，以速度v₀垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图所示。磁感应强度B方向与离子的初速度方向垂直，并垂直于纸面向里。如果离子进入磁场后经过时间t到这位置P，证明：直线OP与离子入射方向之间的夹角θ跟t

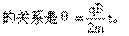
[错解]根据牛顿第二定律和向心加速度公式

[错解原因]高中阶段，我们在应用牛顿第二定律解题时，F应为恒力或平均力，本题中洛伦兹力是方向不断变化的力。不能直接代入公式求解。

[分析解答]

如图，当离子到达位置P时圆心角为

[评析]时时要注意公式的适用条件范围，稍不注意就会出现张冠李戴的错误。如果想用平均力的牛顿第二定律求解，则要先求平均加速度

3.　如图8－15所示，长为l的绝缘细线，一端悬于O点，另一端连接一质量为m的带负电小球，置于水平向右的匀强电场中，在O点

向右水平拉直后从静止释放，细线碰到钉子后要使小球刚好饶钉子O′在竖直平面内作圆周运动，求OO′长度。

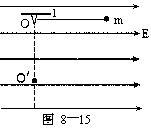
[错解]摆球从A落下经B到C的过程中受到重力G，绳子的拉力T和电场力F_电三个力的作用，并且重力和电场力做功，拉力不做功，由动能定理

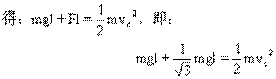
摆球到达最低点时，摆线碰到钉子O′后，若要小球刚好绕钉子O′在竖直平面内做圆周运动，如图8－16。则在最高点D应满足：

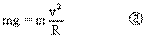
从C到D的过程中，只有重力做功(负功)，由机械能守恒定律

[错解原因]考生以前做过不少“在重力场中释放摆球。摆球沿圆弧线运动的习题”。受到这道题思维定势的影响，没能分析出本题的摆球是在重力场和电场叠加场中运动。小球同时受到重力和电场力的作用，这两个力对摆球运动轨迹都有影响。受“最高点”就是几何上的最高点的思维定势的影响，没能分析清楚物理意义上的“最高点”含义。在重力场中应是重力方向上物体运动轨迹的最高点，恰好是几何意义上的最高点。而本题中，“最高点”则是重力与电场力的合力方向上摆球运动的轨迹的最高点。

[正确解答]本题是一个摆在重力场和电场的叠加场中的运动问题，由于重力场和电场力做功都与路径无关，因此可以把两个场叠加起来看成一个等效力场来处理，如图8－17所示，

∴θ=60°。

开始时，摆球在合力F的作用下沿力的方向作匀加速直线运动，从A点运动到B点，由图8－17可知，△AOB为等边三角形，则摆球从A到B，在等效力场中，由能量守恒定律得：

在B点处，由于在极短的时间内细线被拉紧，摆球受到细线拉力的冲量作用，法向分量v₂变为零，切向分量

接着摆球以v₁为初速度沿圆弧BC做变速圆周运动，碰到钉子O′后，在竖直平面内做圆周运动，在等效力场中，过点O′做合力F的平行线与圆的交点为Q，即为摆球绕O′点做圆周运动的“最高点”，在Q点应满足

过O点做OP⊥AB取OP为等势面，在等效力场中，根据能量守恒定律得：

[评析]用等效的观点解决陌生的问题，能收到事半功倍的效果。然而等效是有条件的。在学习交流电的有效值与最大值的关系时，我们在有发热相同的条件将一个直流电的电压(电流)等效于一个交流电。本题中，把两个场叠加成一个等效的场，前提条件是两个力做功都与路径无关。

2. 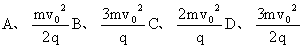如图8－11所示，质量为m，带电量为q的粒子，以初速度v₀，从A点竖直向上射入真空中的沿水平方向的匀强电场中，粒子通过电场中B点时，速率v_B=2v₀，方向与电场的方向一致，则A，B两点的电势差为：

[错解]带电粒子在电场中运动，一般不考虑带电粒子的重力，根据动能定理，电场力所做的功等于带电粒子动能的增量，电势差等于动能增量与电量Q的比值，应选D。

[错解原因]带电粒子在电场中运动，一般不考虑带电粒子的重力，则粒子在竖直方向将保持有速度v₀，粒子通过B点时不可能有与电场方向一致的2v₀，根据粒子有沿场强方向的速度2v0，则必是重力作用使竖直向上的速度变为零。如一定不考虑粒子重力，这只有在电场无限大，带电粒子受电场力的作用，在电场方向上的速度相比可忽略不计的极限状态，且速度沿电场方向才能成立。而本题中v₀与v_B相比不能忽略不计，因此本题应考虑带电粒子的重力。

[分析解答]在竖直方向做匀减速直线运动2gh=v₀²①

根据动能定理

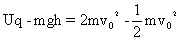
[评析]根据初、末速度或者运动轨迹判断物体的受力情况是解决与运动关系问题的基本功。即使在电学中，带电粒子的运动同样也要应用这个基本功。通过这样一些题目的训练，多积累这方面的经验，非常必要。

复习指导：①回归课本夯实基础，仔细看书把书本中的知识点掌握到位

　　　　 　②练习为主提升技能，做各种类型的习题，在做题中强化知识

　　　　　 ③整理归纳举一反三，对易错知识点、易错题反复巩固

　　　　 　④重视物理学的科学研究方法。本部分内容的主要研究方法有：⑴理想化模型。如点电荷、电场线、等势面；⑵比值定义法。电场强度、电势的定义方法是定义物理量的一种重要方法；⑶类比方法。电场和重力场的比较；电场力和重力的比较；带电粒子在电场中的运动和平抛运动的类比。

　　　　　 ⑤电场力做功的求解方法：⑴由功的定义W=FL求；⑵利用结论“电场力做功等于电荷电势能增量的负值”来求，即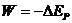；⑶利用求。

　　　　　 ⑥正确分析带电粒子的受力及运动特征是解决问题的前提合外力即初始状态的速度，因此应把带电粒子的运动情况和受力情况结合起来进行分析。当带电粒子在复合场中所受合外力为零时，做匀速直线运动。当带电粒子所受的合外力是变力，且与初速度方向不在一条直线上时，粒子做非匀变速曲线运动，这是粒子的运动轨迹既不是圆弧也不是抛物线，由于带电粒子可能连续通过几个情况不同的复合场区，因此粒子的运动情况也发生相应的变化，其运动的过程可能由几种不同的运动阶段组成。

1.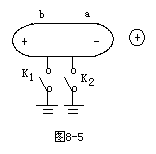 如图8－5所示，把一个不带电的枕型导体靠近带正电的小球，由于静电感应，在a，b端分别出现负、正电荷，则以下说法正确的是：

A．闭合K₁，有电子从枕型导体流向地　　 B．闭合K₂，有电子从枕型导体流向地

C．闭合K₁，有电子从地流向枕型导体　　 D．闭合K₂，没有电子通过K₂

[错解]枕型导体电荷总是守恒的，没有电子流过K₂。选D。

[错解原因]由于对没有正确理解电荷守恒的相对性，所以在本题中认为枕型导体的电荷总是守恒的，便错选答案D。

[分析解答]在K₁，K₂都闭合前，对于枕型导体它的电荷是守恒的，a，b出现的负、正电荷等量。当闭合K₁，K₂中的任何一个以后，便把导体与大地连通，使大地也参与了电荷转移。因此，导体本身的电荷不再守恒，而是导体与大地构成的系统中电荷守恒。由于静电感应，a端仍为负电荷，大地远处感应出等量正电荷，因此无论闭K₁还是K₂，都是有电子从地流向导体，应选答案C。

[评析]在解决此类静电平衡问题时，对电荷守恒的理解应为：电荷守恒定律有相对性，一个物理过程中，某个物体或某些物体的电荷并不守恒，有增或有减，而这一过程中必有另一些物体的电荷有减或有增，其中的增量和减量必定相等，满足全范围内的守恒。即电荷是否守恒要看是相对于哪一个研究对象而言。电荷守恒是永恒的，是不需要条件的。电荷守恒定律也是自然界最基本的规律之一。在应用这个定律时，只要能够全面地考察参与电荷转移的物体，就有了正确地解决问题的基础。