
22. 已知函数
(1)当a=b= 时,求
时,求 的单调递增区间和极值。
的单调递增区间和极值。
(2)当 在x=1,和x=
在x=1,和x= 处取得极值,求
处取得极值,求 的解析式。
的解析式。
(3)当a=b时 在定义域上是单调函数,求a的取值范围。(参考数值:e
在定义域上是单调函数,求a的取值范围。(参考数值:e 2.7)
2.7)
21.设椭圆 =1(a>b>0)的焦点为F1、F2,P是椭圆上任一点,若∠F1PF2的最大值为
=1(a>b>0)的焦点为F1、F2,P是椭圆上任一点,若∠F1PF2的最大值为 .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设直线l与椭圆交于M、N两点,且l与以原点为圆心,短轴长为直径的圆相切.已知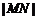 的最大值为4,求椭圆的方程和直线l的方程.
的最大值为4,求椭圆的方程和直线l的方程.
20.某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
|
日 期 |
4月1日 |
4月2日 |
4月3日 |
4月4日 |
4月5日 |
|
温 差 |
10 |
13 |
11 |
12 |
7 |
|
感染数 |
23 |
32 |
24 |
29 |
17 |
(1)求这5天的平均感染数;
(2)从4月1日至4月5日中任取2天,记感染数分别为 用
用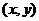 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中 视为同一事件,并求
视为同一事件,并求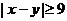 的事件A的概率。
的事件A的概率。
19. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(1)求四棱锥P-ABCD的体积V;
(2)若F为PC的中点,求证PC⊥平面AEF;
(3)求证CE∥平面PAB.
18.已知数列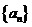 的前
的前 项和
项和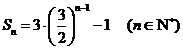 ,数列
,数列 满足:
满足: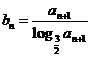
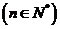 . (1)试求
. (1)试求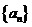 的通项公式,并说明
的通项公式,并说明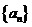 是否为等比数列;
是否为等比数列;
(2)求数列 的前n项和
的前n项和 ; (3)求
; (3)求 的最小值.
的最小值.
17.已知函数 ,且函数
,且函数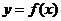 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为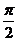 .
.
(1)求 的值; (2)若函数
的值; (2)若函数 在区间
在区间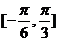 上单调递增,求k的取值范围.
上单调递增,求k的取值范围.
16. 下面四个命题:①命题“ 的否定是“
的否定是“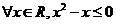 ”;
”;
②把函数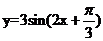 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到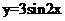 的图象;
的图象;
③函数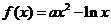 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间; ④正方体的内切球与其外接球的表面积之比为1∶3;
是f(x)的单调递增区间; ④正方体的内切球与其外接球的表面积之比为1∶3;
其中所有正确命题的序号为
15.过抛物线 的焦点
的焦点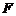 作垂直于
作垂直于 轴的直线,交抛物线于
轴的直线,交抛物线于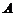 、
、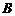 两点,则以
两点,则以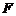 为圆心、
为圆心、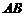 为直径的圆方程是________________.
为直径的圆方程是________________.
14.已知等差数列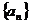 中,有
中,有 成立.类似地,在等比数列
成立.类似地,在等比数列 中,有_____________
中,有_____________ ______________成立.
______________成立.
13.如果复数 的实部和虚部相等,则实数
的实部和虚部相等,则实数 等于
。
等于
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com