
2.圆的标准方程刻画了圆的位置特点(圆心与半径),圆的一般方程反映了圆的代数特点(二元二次方程Ax2+By2+Cxy+Dx+Ey+F=0 A=B≠0,C=0,且D2+E2-4AF>0)。判断点P(x0,y0)与⊙M:(x-a)2+(y-b)2= r2的位置关系,用|PM|与r的大小,即:|PM|>r
A=B≠0,C=0,且D2+E2-4AF>0)。判断点P(x0,y0)与⊙M:(x-a)2+(y-b)2= r2的位置关系,用|PM|与r的大小,即:|PM|>r (x0-a)2+(y0-b)2>
r2
(x0-a)2+(y0-b)2>
r2 P在⊙M外;|PM|<r
P在⊙M外;|PM|<r (x0-a)2+(y0-b)2<
r2
(x0-a)2+(y0-b)2<
r2 P在⊙M内;|PM|=r
P在⊙M内;|PM|=r (x0-a)2+(y0-b)2=
r2
(x0-a)2+(y0-b)2=
r2 P在⊙M上。过两个定点A、B的圆,圆心在线段AB的中垂线上。
P在⊙M上。过两个定点A、B的圆,圆心在线段AB的中垂线上。
[举例1]一圆经过A(4,2),B(-1,3)两点,且在两坐标轴上的四个截距之和为2,则圆的方程为 。
解析:研究圆在坐标轴上的截距,宜用一般方程(因为与圆心、半径没有直接联系),设圆的方程为x2+y2+Dx+Ey+F=0,∵圆过点A、B,∴4D+2E+F+20=0 ①,-D+3E+F+10=0 ②,
圆在x轴上的截距即圆与x轴交点的横坐标,当y=0时,x2+Dx+F=0,x1+x2=-D
圆在y轴上的截距即圆与y轴交点的纵坐标,当x=0时,y2+Ey+F=0,y1+y2=-E
由题意知:-D-E=2 ③,解①②③得D=-2,E=0,F=-12。
[举例2]若存在实数k使得直线 :kx-y-k+2=0与圆C:x2+2ax+y2-a+2=0无公共点,则实数a的取值范围是:
。
:kx-y-k+2=0与圆C:x2+2ax+y2-a+2=0无公共点,则实数a的取值范围是:
。
解析:本题看似直线远的位置关系问题,其实不然。注意到直线 对任意的实数k恒过定点
对任意的实数k恒过定点
M(1,2),要存在实数k使得直线 与⊙C相离,当且仅当M点在圆外;方程x2+2ax+y2-a+2=0
与⊙C相离,当且仅当M点在圆外;方程x2+2ax+y2-a+2=0
变形为:(x+a)2+y2= a2+a-2, M点在⊙C外 (1+a)2+4>a2+a-2>0,解得:-7<a<-2或a>1.
(1+a)2+4>a2+a-2>0,解得:-7<a<-2或a>1.
注:本题中a2+a-2>0是极易疏漏的一个潜在要求。
[巩固1]过点A(3,-2),B(2,1)且圆心在直线x-2y-3=0上的圆的方程是 。
[巩固2]已知定点M(x0,y0)在第一象限,过M点的两圆与坐标轴相切,它们的半径分别为r1,
r2,则r1r2= 。
[迁移] 关于曲线 给出下列说法:①关于直线
给出下列说法:①关于直线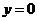 对称;②关于直线
对称;②关于直线 对称;③关于点
对称;③关于点 对称;④关于直线
对称;④关于直线 对称;⑤是封闭图形,面积小于
对称;⑤是封闭图形,面积小于 ;⑥是封闭图形,面积大于
;⑥是封闭图形,面积大于 ;则其中正确说法的序号是
;则其中正确说法的序号是
1.曲线C的方程为:f(x,y)=0 曲线C上任意一点P(x0,y0)的坐标满足方程f(x,y)=0,即f(x0,y0)=0;且以f(x,y)=0的任意一组解(x0,y0)为坐标的点P(x0,y0)在曲线C上。
曲线C上任意一点P(x0,y0)的坐标满足方程f(x,y)=0,即f(x0,y0)=0;且以f(x,y)=0的任意一组解(x0,y0)为坐标的点P(x0,y0)在曲线C上。
依据该定义:已知点在曲线上即知点的坐标满足曲线方程;求证点在曲线上也只需证点的坐标满足曲线方程。求动点P(x,y)的轨迹方程即求点P的坐标(x,y)满足的方程(等式)。求动点轨迹方程的步骤:①建系,写(设)出相关点的坐标、线的方程,动点坐标一般设为(x,y),②分析动点满足的条件,并用等式描述这些条件,③化简,④验证:满足条件的点的坐标都是方程的解,且以方程的解为坐标的点都满足条件。
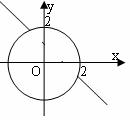 [举例1] 方程
[举例1] 方程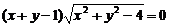 所表示的曲线是: ( )
所表示的曲线是: ( )



A B C D
解析:原方程等价于: ,或
,或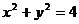 ;
;
其中当 需
需 有意义,等式才成立,即
有意义,等式才成立,即 ,此时它表示直线
,此时它表示直线 上不在圆
上不在圆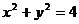 内的部分,这是极易出错的一个环节。选D。
内的部分,这是极易出错的一个环节。选D。
[举例2] 已知点A(-1,0),B(2,0),动点M满足2∠MAB=∠MBA,求点M的轨迹方程。
 解析:如何体现动点M满足的条件2∠MAB=∠MBA
解析:如何体现动点M满足的条件2∠MAB=∠MBA
是解决本题的关键。用动点M的坐标体现2∠MAB=∠MBA
的最佳载体是直线MA、MB的斜率。
设M(x,y),∠MAB= ,则∠MBA=2
,则∠MBA=2 ,它们是直线
,它们是直线
MA、MB的倾角还是倾角的补角,与点M在x轴的上方
还是下方有关;以下讨论:
①
若点M在x轴的上方, 
此时,直线MA的倾角为 ,MB的倾角为
,MB的倾角为 -2
-2 ,
,
 (2
(2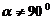 )
)

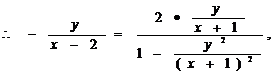
得:
 ,∵
,∵ .
.
当2 时,
时,  =450,
=450,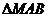 为等腰直角三角形,此时点M的坐标为(2,3),它满足上述方程.
为等腰直角三角形,此时点M的坐标为(2,3),它满足上述方程.
②当点M在x轴的下方时, y<0,同理可得点M的轨迹方程为 ,
,
③当点M在线段AB上时,也满足2∠MAB=∠MBA,此时y=0(-1<x<2).
 综上所求点的轨迹方程为
综上所求点的轨迹方程为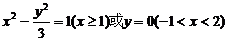 .
.
[巩固1]右图的曲线是以原点为圆心,1为半径的圆的一部分,
则它的方程是
A.( )·(
)·( )=0
)=0
B.( )·(
)·( )=0
)=0
C.( )·(
)·( )=0
)=0
D.( )·(
)·( )=0
)=0
[巩固2]已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足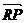 ·
·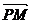 =
=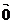 ,2
,2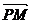 +3
+3 =
=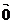 ,当点P移动时,求M点的轨迹方程。
,当点P移动时,求M点的轨迹方程。
[迁移]正方体ABCD-A1B1C1D1的棱长为1,点M是棱AB的中点,点P是平面ABCD上的一动点,且点P到直线A1D1的距离两倍的平方比到点M的距离的平方大4,则点P的轨迹为: A.圆 B.椭圆 C.双曲线 D.抛物线
37.(10分)[思想政治--公民道德与伦理常识]
2004年2月,沈浩被选派到安徽省凤阳县小岗村担任村干部。2006年底,在3年 任职期满时,因98位村民按下挽留的手印,他毅然放弃回城工作,继续留在小岗村任职。在小岗村任职期间,他始终把群众利益放在心上,带领村民修公路、办工业、兴商贸,发展种植、养殖和高效农业,开发农家乐生态旅游,使小岗村的面貌发生了巨大变化。2009年11月6日,年仅45岁的他积劳成疾,猝逝在工作岗位上。沈浩同志以自己的模范言行和突出实绩,赢得了小岗人的信赖和爱戴。
(1)沈浩的事迹是如何体现我国公民道德建设的核心和原则的?(4分)
(2)作为青年学生,我们应该如何向沈浩学习,追求更高层次的道德目标?(6分)




36.(10分)[思想政治--国家和国际组织常识]
第十一届全国人民代表大会第三次会议工作日程安排(节选)

(1)结合上述材料,分析说明十一届全国人民代表大会行使的职权。(4分)
(2)从上述工作日程安排中可以看出全国人大实行什么样的组织活动原则? (2
分)材料是如何体现这一原则的?(4分)
31.(10分)[地理--自然灾害与防治]
进入2010年以来,世界各地地震频发。读下列材料回答问题。
材料一 海地当地时间20 1 0年1月1 2日下午4点53分发生里氏7.3级强烈地震,震源深度约10公里,震中离海地首都太子港只有l 5公里。这次地震造成的死亡人数最终可能超过l0万人。
当地时间2010年2月27日凌晨3时34分,一场里氏8.8级强震撼动了智利中南部以及若干周边国家,震源深度33公里。地震在智利造成的死亡人数超过800人。
材料二 世界地震带分布图

(1)分析海地和智利大地震的共同成因。(4分)
(2)海地地震比智利地震震级小,但造成的人员和财产损失大很多,试分析原因。(6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com