
16.(本小题共13分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,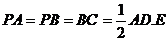 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
 (II)求二面角C-PE-A的余弦值;
(II)求二面角C-PE-A的余弦值;
(III)若四棱锥P-ABCD的体积为4,求AF的长.
15.(本小题共13分)
已知函数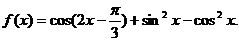
(I)求函数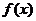 的最小正周期及图象的对称轴方程;
的最小正周期及图象的对称轴方程;
(II)设函数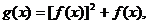 求
求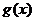 的值域.
的值域.
14.有下列命题:
①若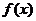 存在导函数,则
存在导函数,则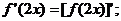
②若函数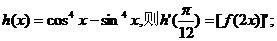
③若函数 ,则
,则
④若三次函数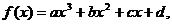 则
则 是“
是“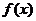 有极值点”的充要条件.
有极值点”的充要条件.
其中真命题的序号是 .
3
13.若A,B,C为 的三个内角,则
的三个内角,则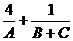 的最小值为
.
的最小值为
.
12.若直线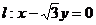 与曲线
与曲线
( 为参数,
为参数, )有两个公共点A,B,且|AB|=2,则实数a的值为
;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为
.
)有两个公共点A,B,且|AB|=2,则实数a的值为
;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为
.
11.若A,B,C是⊙O上三点,PC切⊙O于点C,  ,则
,则 的大小为
.
的大小为
.
9.把容量是100的样本分成8组,从第1组到第4组的频数分别是15,17,11,13,第5组到第7组的频率之和是0.32,那么第8组的频率是 .
 10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 cm3.
10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 cm3.
8.设函数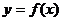 的定义域为R+,若对于给定的正数K,定义函数
的定义域为R+,若对于给定的正数K,定义函数 ,则当函数
,则当函数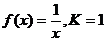 时,定积分
时,定积分 的值为
的值为
( )
A.2ln2+2 B.2ln2-1 C.2ln2 D.2ln2+1
第Ⅱ卷(非选择题 共110分)
7.某单位员工按年龄分为A,B,C三级,其人数之比为5:4:1,现用分层抽样的方法从总体中抽取一个容量为20的样本,已知C组中甲、乙二人均被抽到的概率是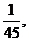 则该单位员工总数为 ( )
则该单位员工总数为 ( )
A.110 B.100 C.90 D80.
6.若椭圆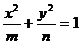 与双曲线
与双曲线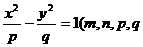 均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则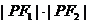 等于 ( )
等于 ( )
A. B.
B.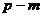 C.
C.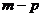 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com