
21.(本小题满分14分)直线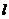 与抛物线
与抛物线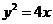 相交于A,B两点,F是抛物线的焦点。
相交于A,B两点,F是抛物线的焦点。
(1)求证:“如果直线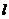 过点T(3,0),那么
过点T(3,0),那么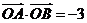 ”是真命题
”是真命题
(2)设 是抛物线上三点,且
是抛物线上三点,且 成等差数列。当AD的垂直平分线与
成等差数列。当AD的垂直平分线与 轴交于点T(3,0)时,求点B的坐标。
轴交于点T(3,0)时,求点B的坐标。
本资料由《七彩教育网》 提供!
贵州省云峰中学09-10学年高二下学期3月月考
20.(本小题满分13分)已知 ,命题
,命题 函数
函数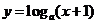 在
在 上单调递减,命题
上单调递减,命题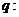 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
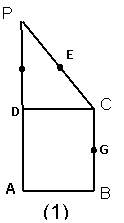
19.(本小题满分12分)如图(1)在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD如图(2)
(1)求二面角G-EF-D的大小;
(2)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明过程.

|
18.(本小题满分12分)
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M,N分别是AB,PC的中点。
(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证:MN⊥平面PCD;
(3)当AB的长度变化时,求异面直线PC与AD所成角的可能范围。
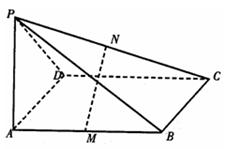
17.(本小题满分12分)如图,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=直线 .
.
(1)求证:BC∥ ;
;
 (2)试判断MN与平面PAD是否平行?并证明你的结论.
(2)试判断MN与平面PAD是否平行?并证明你的结论.
16.(本小题满分12分)如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2, PB=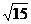 ,PD=
,PD=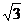 。
。
(1)求证:BD⊥平面PAD;
(2)若PD与底面ABCD成60°的角,试求二面角P-BC-A的大小。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com