
5.从各类土地变化的影响及其原因的分析中,你认为资源优化配置应 ( )
A.发挥宏观调控的基础性作用 B.通过调整所有制结构来实现
C.密切关注自然环境的变化 D.尽量避免市场调节的盲目性
据英国《每日邮报》2010年1月10日报道,有多位权威气候学家推断在未来20年至30年间,地球将经历一个相对气温偏低的“微型冰河世纪”。假设这一推断成立,完成6、7题。
4.分析各类土地变化的影响及原因,错误的是 ( )
A.粮食需求增加导致相关土地比重变化
B.气候变暖是耕地面积增加的主要原因
C.停止垦荒有利于遏制环境恶化的趋势
D.适度生态退耕利于改善农业生产结构
3.1954-2005年,该地 ( )
A.耕地比重上升,其他类型比重下降 B.毁林开荒是耕地增长的最主要方式
C.随着农业科技发展,垦荒速度加快 D.水域比重变化幅度小于其他类型
2.从虚拟水角度看,我国西北干旱地区应 ( )
①大量引入水密集型的产品 ②发展高效节水农业
③调整农业结构 ④优化饮食结构
⑤充分开采地下水 ⑥大规模引用高山融雪水
A.①②③④ B.②⑤⑥ C.②③⑥ D.①②③⑤
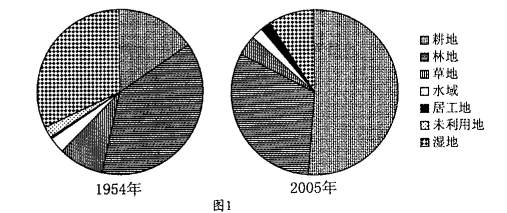 图1示意我国北方某地1954年和2005年土地利用结构。读图完成3-4题。
图1示意我国北方某地1954年和2005年土地利用结构。读图完成3-4题。
1.从生态可持续发展的视角看,以色列农业的发展方向是 ( )
A.粮食种植业为主 B.乳畜业为主 C.园艺业为主 D.家禽饲养业
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题记分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
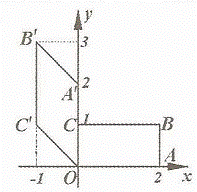
(1)(本小题满分7分)选修4-2:矩阵与变换
如图,矩形 在变换
在变换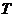 的作用下变成了平行四边形
的作用下变成了平行四边形 ,变换
,变换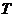 所对应的矩阵为
所对应的矩阵为 ,矩阵
,矩阵 是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵。求
是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵。求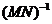 ,并判断矩阵
,并判断矩阵 是否存在特征值。
是否存在特征值。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标平面内,以坐标原点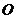 为极点,轴的正半轴为极轴,建立极坐标系。曲线
为极点,轴的正半轴为极轴,建立极坐标系。曲线 的极坐标方程是
的极坐标方程是 ,曲线
,曲线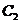 的参数方程是
的参数方程是 (
( 为参数,
为参数, ),求曲线
),求曲线 上的点的曲线
上的点的曲线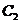 上的点之间距离的取值范围。
上的点之间距离的取值范围。
(3)(本小题满分7分)选修4-5:不等式选讲
已知正实数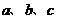 满足
满足 ,不等式
,不等式
 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
20.(本小题满分14分)
我们把半椭圆 与圆弧
与圆弧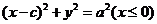 合成的曲线称作“曲圆”,其中
合成的曲线称作“曲圆”,其中 。如图,
。如图,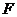 为半椭圆的右焦点,
为半椭圆的右焦点, 和
和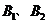 分别是“曲圆”与
分别是“曲圆”与 轴、
轴、 轴的焦点,已知
轴的焦点,已知 ,扇形
,扇形 的面积等于
的面积等于 。
。
(Ⅰ)求“曲圆”的方程;
(Ⅱ)过点F倾斜角为 的直线交“曲圆”于
的直线交“曲圆”于 两点,试将
两点,试将 的周长
的周长 表示为
表示为 的函数;
的函数;
(Ⅲ)当 的周长
的周长 最大时,试探究
最大时,试探究 的面积
的面积 是否为定值?若是,求出
是否为定值?若是,求出 的值;若不是,求出
的值;若不是,求出 的取值范围。
的取值范围。

19.(本小题满分13分)
已知函数 (
( 为常数)在点
为常数)在点 处切线的斜率为
处切线的斜率为 。
。
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数 在区间
在区间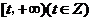 上存在极值,求
上存在极值,求 的最大值;
的最大值;
(Ⅲ)设 ,试问数列
,试问数列 中是否存在
中是否存在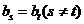 ?若存在,求出所有相等的两项;若不存在,请说明理由
?若存在,求出所有相等的两项;若不存在,请说明理由
18.(本小题满分13分)
图1是长方体截去一个角后得到的几何体,其中底面 是正方形,
是正方形,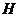 为
为 中点,图2是该几何体的侧视图。
中点,图2是该几何体的侧视图。
(Ⅰ)判断两直线 与
与 的位置关系,并给予证明;
的位置关系,并给予证明;
(Ⅱ)求直线 与平面
与平面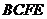 所成角的大小;
所成角的大小;
(Ⅲ)是否存在点 ,使得
,使得 ,且二面角
,且二面角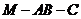 的大小为
的大小为 ?若存在,求不存在,请说明理由。
?若存在,求不存在,请说明理由。

17.(本小题满分13分)
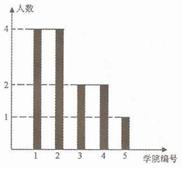
上海世博会举办时间为2010年5月1日-10月31日。福建馆以“海西”为参博核心元素,主题为“潮涌海西,魅力福建”。福建馆招募了60名志愿者,某高校有l3人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所所学院(这5所学院编号为1-5号),人员分布如图所示。
若从这13名入选者中随机抽取3人。
(Ⅰ)求这3人所在学院的编号恰好成等比数列的概率;
(Ⅱ)求这3人中中英文讲解员人数的分布列及数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com