
2.关于函数 ,下列说法正确的是( B )
,下列说法正确的是( B )
(A)当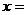 -2时,
-2时, 有极大值1 (B)
当
有极大值1 (B)
当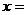 0时,
0时, 有极小值-63
有极小值-63
(C)当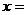 2时,
2时, 有极大值1 (D)
函数的最大值为1
有极大值1 (D)
函数的最大值为1
1.下列函数中,在x=0处的导数不等于零的是( A )
A.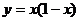 B.
B.
C.y=ln(1-x2) D.
例1.设函数 内为奇函数且可导,证明:
内为奇函数且可导,证明:
 内的偶函数.
内的偶函数.
证明:对任意
由于 为奇函数,
为奇函数, ,
,
于是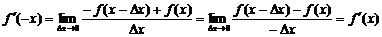 ,
,
因此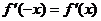 即
即 内的偶函数。
内的偶函数。
例2.已知函数 处取得极值,并且它
处取得极值,并且它
的图象与直线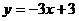 在点(1,0)处相切,求a、b、c的值.
在点(1,0)处相切,求a、b、c的值.
解:由曲线 过(1,0)得
过(1,0)得 ①
又
①
又 +b
+b
则 ②
②
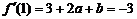 ③
③
解①②③得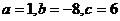 .
.
例3.已知 有极大值
有极大值 和极小值
和极小值 .
.
(1)求 +
+ 的值;
的值;
(2)设曲线 的极值点为A、B,求证:线段AB的中点在
的极值点为A、B,求证:线段AB的中点在 上.
上.
解:(1) ,由于
,由于 有极大值和极小值,
有极大值和极小值,
 、
、 的两根,则
的两根,则


(2)设 ,由
,由

 知AB的中点在
知AB的中点在 上。
上。
例4.设函数 的驻点是0和4.
的驻点是0和4.
(1)求常数k的值;
(2)确定函数 的单调区间;
的单调区间;
(3)求 的极值。
的极值。
解:(1) ,由于驻点是0和4,∴0和4是方程
,由于驻点是0和4,∴0和4是方程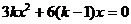 的两根,可求得
的两根,可求得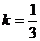
(2)由(1)可知 ,∴当
,∴当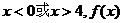 为增函数,
为增函数,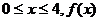 为减函数;
为减函数;
(3)由(2)可判断极大值为 极小值为
极小值为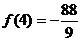
例5.求证:

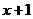 。
。
证明:(1)当 时,
时, =1,
=1,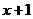 =1,命题成立;
=1,命题成立;
(2)当 >0时,令
>0时,令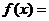

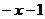 ,则
,则 >0
>0
 在(0,
在(0,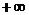 )上为增函数
)上为增函数
 >0,
>0, >
>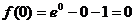 即
即
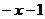 >0
>0
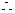
 >
>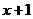 ;
;
(3)当 <0时,令
<0时,令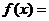

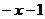 ,则
,则 <0
<0
 在(
在( )上为减函数
)上为减函数
 <0,
<0, >
>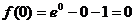 即
即
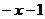 >0
>0
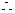
 >
>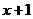
综合以上情况,

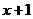 。
。
例6.已知函数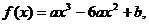 问是否存在实数a、b使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间
. 若不存在,请说明理由 .
问是否存在实数a、b使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间
. 若不存在,请说明理由 .
解: (舍)
(舍)
(1)a>0时,如下表
|
x |
(-1,0) |
0 |
(0,2) |
 |
+ |
0 |
- |
 |
 |
最大值3 |
 |
∴当x=0时, 取得最大值,
∴b=3;
取得最大值,
∴b=3;
(2)a<0时,如下表
|
x |
(-1,0) |
0 |
(0,2) |
 |
- |
0 |
+ |
 |
 |
最小值-29 |
 |
∴当x=0时, 取得最小值,
∴b=-29(9分)
又f(2)=-16a-29, f(-1)=-7a-29<f(2)
取得最小值,
∴b=-29(9分)
又f(2)=-16a-29, f(-1)=-7a-29<f(2)
∴当x=2时,  取得最大值,∴-16a-29=3, a=-2,
取得最大值,∴-16a-29=3, a=-2,
综上:a=2, b=3 或a=-2, b=-29。
例7.(2003年普通高等学校招生全国统一考试(天津卷、辽宁卷理19))
设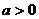 ,求函数
,求函数 的单调区间.
的单调区间.
分析:本例主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力。
解: .
.
当 时
时  .
.

(i)当 时,对所有
时,对所有 ,有
,有 .
.
即 ,此时
,此时 在
在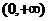 内单调递增.
内单调递增.
(ii)当 时,对
时,对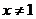 ,有
,有 ,
,
即 ,此时
,此时 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数 在x=1处连续,因此,函数
在x=1处连续,因此,函数 在(0,+
在(0,+ )内单调递增
)内单调递增
(iii)当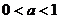 时,令
时,令 ,即
,即 .
.
解得 .
.
因此,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 内也单调递增.
内也单调递增.
令 ,
,
解得 .
.
因此,函数 在区间
在区间 内单调递减.
内单调递减.
例8.⑴ 设 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤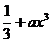 .
.
⑵ 设 ≤1,
≤1, ,求证:
,求证: ≤
≤ .
.
解:⑴
x≤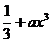 可化为
可化为 ≥0,令
≥0,令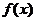 =
= ,
,
 ,由
,由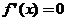 得,
得,
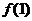 =3a-2≥0,
=3a-2≥0, =-3a+4≥0,∴
=-3a+4≥0,∴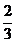 ≤
≤ ≤
≤ , ①
, ①
∴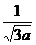 ∈[-1,1],
∈[-1,1],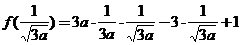 ≥0,即
≥0,即 ≥
≥ ②
②
由①、②得, .
.
从而当 ≤1时,
≤1时, =
= ≥0,即x≤
≥0,即x≤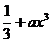 .
.
⑵ 由⑴知,对 ≤1,有
≤1,有 ≤
≤ ,(i=1,2,…,n)
,(i=1,2,…,n)
将这n个式子求和,得 ≤
≤ .
.
例9.从边长为2a的正方形铁片的四个角各截去一个边为x的正方形,再将四边向上折起,做成一个无盖的长方形铁盒,要求长方体的高度与底面边的比值不超过常数t(t>0)。试问当x取何值时,容量V有最大值。

解: =
=
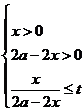
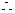

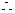 函数V(
函数V( )=
)= 的定义域为
的定义域为
 令
令 =0 得
=0 得 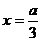
(1)当
 ,即
,即 时,
时, 时,
时, >0 .V(
>0 .V( )为增函数;
)为增函数;

 时,
时, <0 .V(
<0 .V( )为减函数;
)为减函数;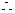 V(
V( )在
)在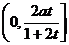 上有极大值V(
上有极大值V( ),
),

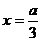 为唯一驻点,
为唯一驻点,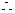 当
当
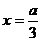 时,
时,  有最大值
有最大值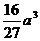 。
。
(2)当
 ,即
,即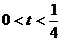 时,
时, 时,
时, >0恒成立;
>0恒成立;
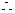 V(
V( )为增函数;
)为增函数; 当
当 时,
时,  有最大值
有最大值 。
。
例10.某银行准备新设一种定期存款业务,经预测,存款量与利率的平方成正比,比例系数为K(K>0),贷款的利率为4.8%,又银行吸收的存款能全部放贷出去.(1)若存款的利率为x,x (0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);(2)存款利率定为多少时,银行可获得最大收益?
(0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);(2)存款利率定为多少时,银行可获得最大收益?
解:(1)由题意,存款量g(x)=Kx2,银行应支付的利息
h(x)=x·g(x)= Kx3
(2)设银行可获收益为y,则y=0.048·Kx2–Kx3
y /=K·0.096x–3 Kx2 令y /=0 即K×0.096x–3 Kx2=0
解得x=0 或x=0.032
又当x (0,0.032)时,y />0, x
(0,0.032)时,y />0, x (0.032,0.048)时, y /<0
(0.032,0.048)时, y /<0
 y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
故当x=0.032时,y在(0,0.048)内取得极大值,亦即最大值
答:存款利率为3.2%时,银行可获得最大收益
求闭区间 上的可导函数的最大(小)值的方法是:首先求出此函数在开区间
上的可导函数的最大(小)值的方法是:首先求出此函数在开区间 内的驻点,然后计算函数在驻点与端点处的值,并将它们进行比较,其中最大的一个即为最大值,最小的一个即为最小值,这里无须对各驻点讨论其是否为极大(小)值点。
内的驻点,然后计算函数在驻点与端点处的值,并将它们进行比较,其中最大的一个即为最大值,最小的一个即为最小值,这里无须对各驻点讨论其是否为极大(小)值点。
如果函数不在闭区间 上可导,那么求函数的最大(小)值时,不仅要比较此函数在各驻点与端点处的值,还要比较函数在定义域内各不可导的点处的值。
上可导,那么求函数的最大(小)值时,不仅要比较此函数在各驻点与端点处的值,还要比较函数在定义域内各不可导的点处的值。
一般地,求在闭区间 上连续,在开区间
上连续,在开区间 内可导的函数
内可导的函数 在闭区间
在闭区间 上最值的步骤为:
上最值的步骤为:
⑴求 在区间
在区间 内的根,即导数为0的点(不必确定它是极大值点还是极小值点),求出这些导数为0的点的函数值;
内的根,即导数为0的点(不必确定它是极大值点还是极小值点),求出这些导数为0的点的函数值;
⑵求 在闭区间
在闭区间 两端点处的函数值,即
两端点处的函数值,即 与
与 ;
;
⑶将导数为0的函数值与两端点处的函数值进行比较,其中最大的一个即为最大值,最小的一个即为最小值。
若函数 在某个区间内可导,则当
在某个区间内可导,则当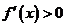 时,
时, 在此区间上为单调增函数;而当
在此区间上为单调增函数;而当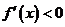 时,
时, 在此区间上为单调减函数。利用上述性质,可以研究函数的单调性。
在此区间上为单调减函数。利用上述性质,可以研究函数的单调性。
注意点:
(1)同一函数的两个单调区间不能并起来
(2)求函数的单调区间,求导的方法不是唯一的方法,也不一定是最好的方法,但它是一种一般性的方法。
破釜沉舟!!攻克语音关!(16)
|
280 |
降幂 |
|
290 |
冒顿 |
|
|
281 |
青苔 |
|
291 |
冠心病 |
|
|
282 |
青睐 |
|
292 |
削减 |
|
|
283 |
青蒿 |
|
293 |
匍匐 |
|
|
284 |
驾驭 |
|
294 |
咯血 |
|
|
285 |
亲昵 |
|
295 |
咳嗽 |
|
|
286 |
亲家 |
|
296 |
哀戚 |
|
|
287 |
亲戚 |
|
297 |
哂纳 |
|
|
288 |
俊俏 |
|
298 |
哈达 |
|
|
289 |
俨然 |
|
299 |
哪吒 |
|
7.请用一句话为这则新闻拟一个标题,概括新闻的主要内容,不超过20字。(4分)
针对今年入春以来我国北方地区沙尘天气较为频繁的情况,中央气象台副台长肖子牛18日接受记者采访时说,气温偏高、降水偏少和冷空气频繁这三大因素是“祸首”。
气温显著偏高。2006年3月以来,我国北方地区平均气温为3.6摄氏度,比常年同期(2.9摄氏度)偏高0.7摄氏度。其中,西北地区东部、华北大部、黄淮及内蒙古中西部、新疆北部等地气温比常年同期偏高1至2摄氏度,部分地区偏高2至4摄氏度。由于气温回升,致使地表层解冻,土壤水分蒸发大,土质疏松,为初春沙尘天气频繁发生提供了条件。
降水持续偏少。3月份至今,北方地区干旱少雨,其区域平均降水量只有常年同期的75%。其中,秦岭及黄河以北大部地区降水量不足10毫米,青藏高原北部以及内蒙古西部、新疆东南部等地基本无降水。与常年同期相比,华北大部、西北部分地区及内蒙古大部降水量偏少5至8成,部分地区偏少达8成以上。由于干旱少雨,加之气温回升,使地表土质干土层增厚,一遇大风天气极易产生沙尘。
5.依次填入下面一段文字横线处的语句,与上下文衔接最恰当的一组是 ( )
发射定在凌晨。 。火箭 ,如同一条喷吐着烈焰的蛟龙,映红了整个山谷。 ,将塔架导流槽内的蓄水化作一团浓雾,天女散花般四处散开。短短几秒钟,火箭精灵般地钻入了云层。我的眼睛追随着箭尾,突然热泪盈盈。
①沉睡的群山,深邃的夜空,被一声轰鸣突然惊醒②一声轰鸣,突然惊醒沉睡的群山和深邃的夜空
③拔地而起,以雷霆万钧之势④以雷霆万钧之势,拔地而起⑤喷射的火焰 ⑥火焰喷射
A.②④⑥ B.②③⑥ C.①③⑤ D.①④⑤
4.下列各句中没有语病的一句是
A.每个网络使用者都体验过美国专家说的网络“黑洞”,网页毫无原因地无法打开,电子邮件莫名其妙地丢失,原因都可能是由于网络“黑洞”所致。
B.9月26日10时20分,航天员翟志刚和刘伯明开始在神舟七号飞船轨道舱进行轨道舱状态检查和舱外航天服的组装与测试等工作。
C.作为收藏纪念品,2008年北京奥运会金银纪念币以其高纯度的含金量、精美的工艺、严肃的选题和高科技的制造技术,深受收藏爱好者的追捧。
D.省财政厅紧急下拨专款386万元,支持困难地区做好婴幼儿奶粉事件免费医疗救治工作,以确保因资金问题影响对患者的及时救治。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com