
5.已知函数 和
和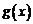 的图象关于原点对称,且
的图象关于原点对称,且 .
.
(Ⅰ)求函数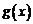 的解析式;
的解析式;
(Ⅱ)解不等式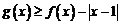 ;
;
(Ⅲ)若 在
在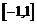 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识,以及综合运用所学知识分析和解决问题的能力.满分14分.
解:(Ⅰ)设函数 的图象上任意一点
的图象上任意一点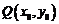 关于原点的对称点为
关于原点的对称点为 ,则
,则
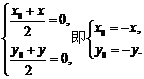
∵点 在函数
在函数 的图象上
的图象上
∴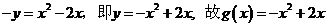
(Ⅱ)由
当 时,
时,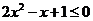 ,此时不等式无解.
,此时不等式无解.
当 时,
时,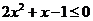 ,解得
,解得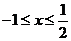 .
.
因此,原不等式的解集为 .
.
(Ⅲ)
①
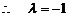
②
ⅰ)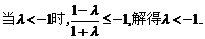
ⅱ)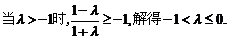
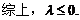
4.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识,考查解析几何的基本思想方法和综合解题能力.满分14分.
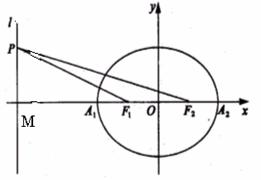
解:(Ⅰ)设椭圆方程为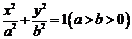 ,半焦距为
,半焦距为 ,则
,则

(Ⅱ)

3.(本小题满分14分)
已知不等式 为大于2的整数,
为大于2的整数,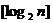 表示不超过
表示不超过 的最大整数. 设数列
的最大整数. 设数列 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明
(Ⅱ)猜测数列 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当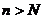 时,对任意b>0,都有
时,对任意b>0,都有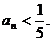
本小题主要考查数列、极限及不等式的综合应用以及归纳递推的思想.
(Ⅰ)证法1:∵当
即
于是有 
所有不等式两边相加可得 
由已知不等式知,当n≥3时有,
∵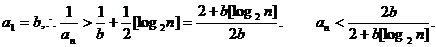
证法2:设 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式

(i)当n=3时, 由 
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即
则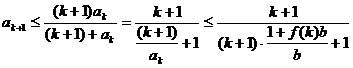

即当n=k+1时,不等式也成立.
由(i)、(ii)知,
又由已知不等式得 
(Ⅱ)有极限,且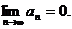
(Ⅲ)∵
则有
故取N=1024,可使当n>N时,都有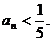
2.(本小题满分12分)
设A、B是椭圆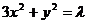 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.
(Ⅰ)解法1:依题意,可设直线AB的方程为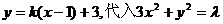 ,整理得
,整理得 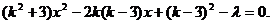 ①
①
设 是方程①的两个不同的根,
是方程①的两个不同的根,
∴ ②
②
且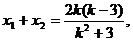 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得

解得k=-1,代入②得,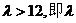 的取值范围是(12,+∞).
的取值范围是(12,+∞).
于是,直线AB的方程为
解法2:设 则有
则有
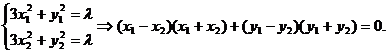
依题意,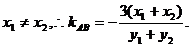
∵N(1,3)是AB的中点, ∴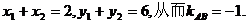
又由N(1,3)在椭圆内,∴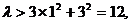
∴ 的取值范围是(12,+∞).
的取值范围是(12,+∞).
直线AB的方程为y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法1:∵CD垂直平分AB,∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得 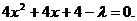
又设 CD的中点为
CD的中点为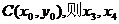 是方程③的两根,
是方程③的两根,
∴
于是由弦长公式可得 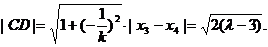 ④
④
将直线AB的方程x+y-4=0,代入椭圆方程得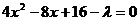 ⑤
⑤
同理可得  ⑥
⑥
∵当 时,
时,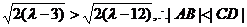
假设存在 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为 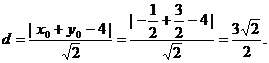 ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得

故当 >12时,A、B、C、D四点匀在以M为圆心,
>12时,A、B、C、D四点匀在以M为圆心,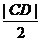 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:)
A、B、C、D共圆 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角 |AN|2=|CN|·|DN|,
|AN|2=|CN|·|DN|,
即  ⑧
⑧
由⑥式知,⑧式左边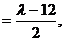
由④和⑦知,⑧式右边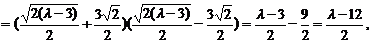
∴⑧式成立,即A、B、C、D四点共圆.
解法2:由(Ⅱ)解法1及λ>12,
∵CD垂直平分AB, ∴直线CD方程为 ,代入椭圆方程,整理得
,代入椭圆方程,整理得
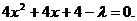 ③
③
将直线AB的方程x+y-4=0,代入椭圆方程,整理得
 ⑤
⑤
解③和⑤式可得
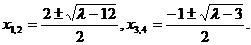
不妨设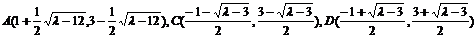
∴

计算可得 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又B为A关于CD的对称点,∴A、B、C、D四点共圆.
(注:也可用勾股定理证明AC⊥AD)
1.(本小题满分14分)
如图,设抛物线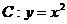 的焦点为F,动点P在直线
的焦点为F,动点P在直线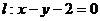 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
解:(1)设切点A、B坐标分别为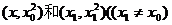 ,
,
∴切线AP的方程为:
切线BP的方程为:
解得P点的坐标为:
所以△APB的重心G的坐标为 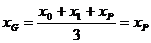 ,
,
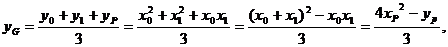
所以 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:

(2)方法1:因为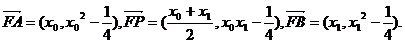
由于P点在抛物线外,则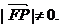
∴
同理有
∴∠AFP=∠PFB.
方法2:①当 所以P点坐标为
所以P点坐标为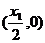 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
即
所以P点到直线BF的距离为:
所以d1=d2,即得∠AFP=∠PFB.
②当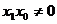 时,直线AF的方程:
时,直线AF的方程: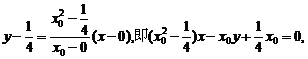
直线BF的方程:
所以P点到直线AF的距离为:
 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离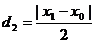 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
某公司到省人才中心招聘销售部工作人员。应聘者很多,但招聘单位却只留给一个职位。在应聘者抢占座位作准备时,一个叫张媛媛的女大学生却几次主动让座,让别人先面试。到她面试时,公司负责人对她的条件虽较为满意,但认为她过于谦让,不适合到销售部工作。该负责人认为,谦让的确是一种美德,但面对激烈的市场竞争。公司更需要“锐意进取”的员工。而张媛媛则认为不具备良好道德修养的人,是干不好工作的。此事在省城引起强烈反响。人们议论纷纷,有人说公司的要求符合市场经济的规则,有人则认为张媛媛的做法是正确的,应继续保持这种美德。
请全面理解材料,但可以从一个侧面、一个角度构思作文。自主确定立意
确定文体,确定标题,写一篇不少于八百字的文章;不要脱离材料内容或其含意范围作文,不要套作,不得抄袭。
山东省新泰一中北校09-10学年高二下学期4月检测
17.下面这首小诗在对“树”进行描述时涉及了作者对“岁月”的思考,请选择另外两种事物,仿照例句的表达方式和句式,各写一句话,描述事物时须改成涉及对“生命”的思考。(4分)
例句:树:如果你挺直了你的身躯,风会比你矮很多,伟岸就会溢满你的岁月。
答:(1)
(2)
16.根据下列材料,用简洁的语言,解释材料中“拼”的含义。(15字以内)(4分)
眼下,“拼生活”成为一种社会时尚。例如,刚毕业的陈明就和两个同班同学“拼房”--l500元人民币的房租 分成三份,每人都能省下一大笔钱。
拼生活,囊括生活的方方面面:“拼卡”一起到商场买东西,优惠卡、购物返券各取所需,赚商家的钱;“拼杂志”--你买《ELLE》,我买《瑞丽》,交换着看……
从这些例子中,我们大致可以推断出“拼”在这里的含义。
答:含义是:
15.默写填空(每空1分,共10分)
(1)吾所以为此者, 。《廉颇蔺相如列传》
(2) ,六宫粉黛无颜色。《长恨歌》
(3) ,江月年年只相似。《春江花月夜》
(4)细草微风岸, 。 月涌大江流。《旅夜书怀》
(5)女娲炼石补天处, 。《李凭箜篌引》
(6) ,草色遥看近却无。《早春呈水部张十八员外》
(7)怀旧空吟闻笛赋,到乡翻似烂柯人。 ,
。《酬乐天扬州初逢席上见赠》
(8)溪云初起日沉阁, 。《咸阳城西楼晚眺》
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com