
5.已知条件p:x≤1,条件q: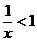 ,则
,则 p是q的 ▲ .条件.
p是q的 ▲ .条件.
4. 某算法的伪代码如右:则输出的结果是 ▲ .
3.函数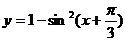 的最小正周期是 ▲ .
的最小正周期是 ▲ .
2. 已知虚数z满足等式:
已知虚数z满足等式: 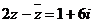 ,则
,则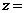 ▲ .
▲ .
1.若集合 ,
,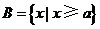 满足
满足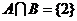 ,则实数a= ▲ .
,则实数a= ▲ .
24. (1)设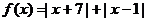
则有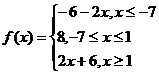 ------ 1分
------ 1分
当 时
时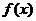 有最小值8
------ 2分
有最小值8
------ 2分
当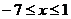 时
时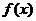 有最小值8 ----- 3分
有最小值8 ----- 3分
当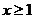 时
时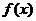 有最小值8
----- 4分
有最小值8
----- 4分
综上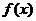 有最小值8
----- 5分
有最小值8
----- 5分
所以 ------6分
------6分
(2)当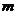 取最大值时
取最大值时
原不等式等价于: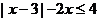 ----- 7分
----- 7分
等价于: 或
或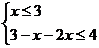 ----- 8分
----- 8分
等价于: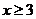 或
或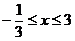 -------- 9分
-------- 9分
所以原不等式的解集为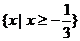 ------ 10分
------ 10分
23. (1)圆心坐标为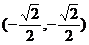 ---- 1分
---- 1分
设圆心的极坐标为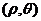
则 ------ 2分
------ 2分
所以圆心的极坐标为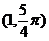 ------ 4分
------ 4分
(2)直线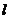 的极坐标方程为
的极坐标方程为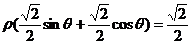
 直线
直线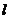 的普通方程为
的普通方程为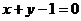 ------ 6分
------ 6分
 圆上的点到直线
圆上的点到直线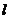 的距离
的距离
即 -------7分
-------7分
 圆上的点到直线
圆上的点到直线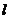 的最大距离为
的最大距离为 ------ 9分
------ 9分

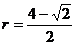 ----- 10分
----- 10分
22. (1)连接 ,则
,则 ------ 1分
------ 1分
又
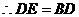 -------- 2分
-------- 2分
又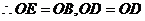
 ------ 4分
------ 4分
 --- 5分
--- 5分
 四点共圆。
------ 6分
四点共圆。
------ 6分
(2)延长 交圆于点
交圆于点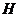
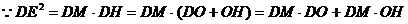 ----- 8分
----- 8分
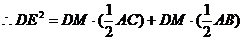 ---- 9分
---- 9分
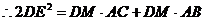 ---- 10分
---- 10分
20. (1)将点(1,1)代入 ,得
,得 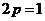
 抛物线方程为
抛物线方程为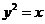 ---- 1分
---- 1分
设 ,
,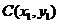
与抛物线方程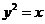 联立得:
联立得: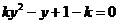 ---- 2分
---- 2分

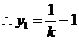

 ----- 3分
----- 3分
由题意有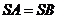 ,
,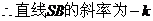
 -----4分
-----4分
 -----5分
-----5分
(2)设
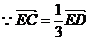
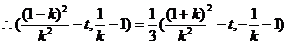
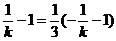
 ------
7分
------
7分
 ----8分
----8分
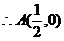
同理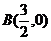 ----10分
----10分
 ----- 11分
----- 11分
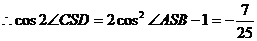 ----- 12分21.解:解:(Ⅰ) 由
----- 12分21.解:解:(Ⅰ) 由 ,得
,得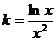 。
。
令
所以,方程 在区间
在区间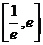 内解的个数即为
内解的个数即为
函数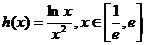 的图像与直线
的图像与直线 交点的个数。
交点的个数。
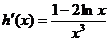
当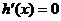 时,
时, 
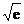 .
----
2分
.
----
2分
当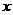 在区间
在区间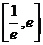 内变化时,
内变化时, 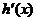 ,
, 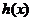 变化如下:
变化如下:
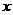 |
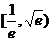 |
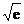 |
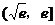 |
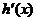 |
+ |
0 |
- |
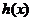 |
增 |
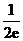 |
减 |
当 时,
时,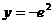 ;当
;当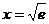 时,
时, ;当
;当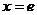 时,
时, 。
。
-------------4分
所以,
(1)当 或
或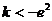 时,该方程无解;
时,该方程无解;
(2)当 或
或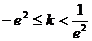 时,该方程有一个解;
时,该方程有一个解;
(3)当 时,该方程有两个解。 ----------- 6分
时,该方程有两个解。 ----------- 6分
(Ⅱ) 由(Ⅰ)知 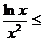
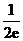 ,∴
,∴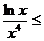
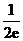
 .
.
∴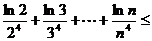
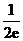
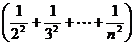 .
-------
8分
.
-------
8分
∴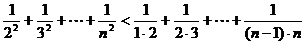
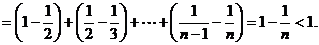 ------
10分
------
10分
∴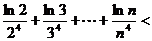
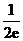 .
.
∵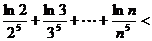
 .
.
∴ 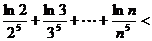
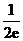 . -----
12分
. -----
12分
三 17.解:(Ⅰ) ------- 1分
------- 1分
依题意
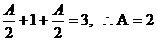
 ------2分
------2分
又 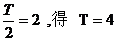
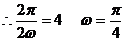 -------3分
-------3分
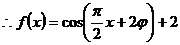
令 x=0,得 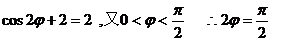 -------4分
-------4分
所以函数 的解析式为
的解析式为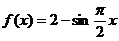 -------6分
-------6分
(还有其它的正确形式,如: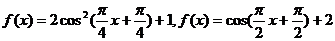 等)
等)
(Ⅱ)当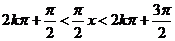 ,
,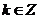 时
时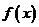 单调递增 -----8分
单调递增 -----8分
即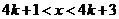 ,
,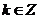 ------1
------1 0分
0分
∴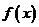 的增区间是
的增区间是 -------12分
-------12分
(注意其它正确形式,如:区间左右两端取闭区间等)
18.解:(Ⅰ) 连接  ,显然
,显然 ------
1分
------
1分
设 ,则
,则 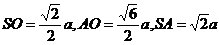
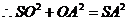 ,
,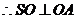 ----- 2分
----- 2分
又 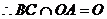 ,
, 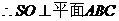 ------
3分
------
3分
(Ⅱ)以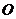 为原点,以
为原点,以 所在射线为
所在射线为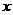 轴正半轴,以
轴正半轴,以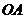 所在射线为
所在射线为 轴正半轴,以
轴正半轴,以 所在射线为
所在射线为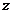 轴正半轴建立空间直角坐标系. 高.考.资/源/网
轴正半轴建立空间直角坐标系. 高.考.资/源/网
则有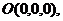
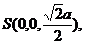
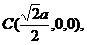

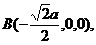



 异面直线
异面直线  所成角的余弦值为
所成角的余弦值为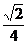 ------5分
------5分
(Ⅲ)假设存在 满足条件,设
满足条件,设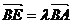
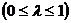 ,则
,则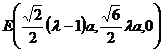 ,
,
则 . --------------7分
. --------------7分
设面 的法向量为
的法向量为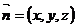 ,
,
由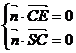 ,
, 得
得 ,
,
取 . -------------9分
. -------------9分
因为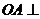 面
面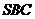 ,所以可取向量
,所以可取向量 为面
为面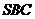 的法向量。高.考.资/源/网
的法向量。高.考.资/源/网
所以,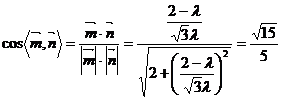 ,
,
解得,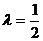 。 -------11分
。 -------11分
所以,当 时,二面角
时,二面角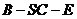 的余弦值为
的余弦值为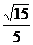 。 -----12分
。 -----12分
19(1)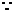 P
P =
=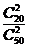 ,
,
P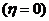 =
=

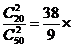
 -------
1分
-------
1分
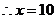 --------- 2分
--------- 2分
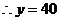
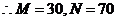
 -----------3分
-----------3分
画出列联表的等高条形图 -------4分
由列联表的等高条形图可以初步判断药物有效 ----5分
(2) 取值为0,1,2
取值为0,1,2
P =
=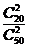 =
= ,
,
P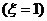 =
= =
= ,
,
P =
=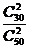 =
= ,
,
 |
0 |
1 |
2 |
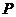 |
 |
 |
 |

 -----7分
-----7分
P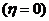 =
= =
=
P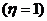 =
=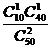 =
=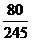
P =
=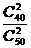 =
=
 |
0 |
1 |
2 |
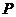 |
 |
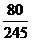 |
 |

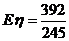 ------9分
------9分

 说明药物有效
----10分
说明药物有效
----10分
(3)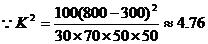 ---------11分
---------11分
由参考数据知不能够以97.5%的把握认为药物有效。 ------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com