
· interpreting the theme
· expressing the culture
·Meaning:
the treasure of the sea
the good-will ambassador of Shanghai Expo.
· 73 :
74
echoing with the color of its body
a typical lucky name in Chinese tradition
(16)(本小题12分)
设△ABC的三个内角A、B、C的对边分别为a、b、c,若B=60°,且 ,
,
(1)求△ABC的面积;
(2)若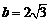 ,求a、c.
,求a、c.
(17)(本小题12分)
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都等于底面的边长。
(1)求证:AC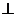 SD;
SD;
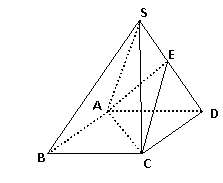 (2)E是侧棱SD的中点, 求SB与CE所成角的正弦.
(2)E是侧棱SD的中点, 求SB与CE所成角的正弦.
(18)(本小题12分)
为了迎接2010上海世博会,某网站举行了一次“世博会知识竞赛”,共有800人参加,随机地编号为001,002,……800。为了解本次竞赛的成绩情况,从中抽取了50人的成绩(得分均为整数,满分100分)进行统计,这50人考试成绩全部介于60分到100分之间,将考试成绩按如下方式分成8组,第一组[60,65),第二组[6 5,70)……第八组[95,100],得到的频率分布直方图如图.
5,70)……第八组[95,100],得到的频率分布直方图如图.
(1)若抽取的50个样本是用系统抽样的方法得到,且第一段抽到的号码为002,则第三段抽到的号码是多少?
 (2)若从考试成绩属于第6组和第8组的所有人中随机抽取2人,设他们的成绩为x,y,求满足
(2)若从考试成绩属于第6组和第8组的所有人中随机抽取2人,设他们的成绩为x,y,求满足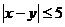 的事件的概率。
的事件的概率。
(19) (本小题满分13分)
已知数列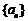 是等差数列,且a2=7, a5=16, 数列
是等差数列,且a2=7, a5=16, 数列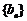 是
是 各项为正数的数列,且
各项为正数的数列,且 ,点
,点 在直线y=x+1上.
在直线y=x+1上.
(1)求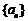 、
、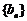 的通项公式;
的通项公式;
(2)设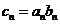 ,求数列
,求数列 的前
的前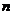 项的和Sn .
项的和Sn .
(20)(本小题满分13分)
已知函数 ,且
,且 ,
,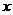 =1是它的极值点.
=1是它的极值点.
(1) 求f(x)的表达式;
(2)
试确定f(x)的单调区间 ;
;
(3)若函数 恰有3个零点,求
恰有3个零点,求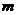 的取值范围.
的取值范围.
(21)(本小题13分)
21. 椭圆 的中心在原点,过点
的中心在原点,过点 ,且右焦点
,且右焦点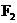 与圆
与圆 的圆心重合.
的圆心重合.
(1)求椭圆C1的方程;
(2)若点 P是椭圆上的动点,EF是圆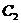 的任意一条直径,求
的任意一条直径,求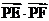 的最大值.
的最大值.
 (3)过点
(3)过点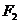 的直线
的直线 交椭圆于M、N两点,问是否存在
交椭圆于M、N两点,问是否存在 这样的直线
这样的直线 ,使得以MN为直径的圆过椭圆的左焦点
,使得以MN为直径的圆过椭圆的左焦点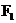 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由;
的方程;若不存在,请说明理由;
湖南省常德市2010届高三下学期4月月考
15.定义区间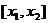 的长度为
的长度为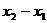 ,已知函数
,已知函数 的定义域
的定义域 为
为 ,值域为
,值域为 ,则区间
,则区间 的长度的最大值为 ,最小值为 .
的长度的最大值为 ,最小值为 .
14.设 ,则关于
,则关于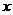 的方程
的方程 在
在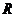 上有实数根的概率为
.
上有实数根的概率为
.
13..将函数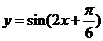 的图象向左平移
的图象向左平移 个单位,再向下平移1个单位,所得到的函数解析式为 .
个单位,再向下平移1个单位,所得到的函数解析式为 .
12.已知正数 满足
满足 ,则
,则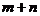 的最小值为 .
的最小值为 .
11.已知函数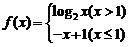
 ,则满足
,则满足 时,
时,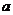 的取值范围是 (-1,4) .
的取值范围是 (-1,4) .
10.已知 =(2,-1),
=(2,-1),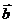 =(m,4),若
=(m,4),若 ,则m=
,则m=
9.若复数(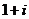 )2=a+bi(a、
)2=a+bi(a、 为实数)则
为实数)则  = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com