
1.下列关于细胞内化合物的叙述中,正确的是 ( )
A.淀粉是植物细胞壁的主要成分,它的基本组成单位是葡萄糖
B.蛋白质是生命活动的主要承担者,它的基本组成单位是氨基酸
C.DNA是一切生物的遗传物质,它的基本组成单位是脱氧核苷酸
D.磷脂是细胞膜的主要成分,它的基本组成单位是甘油和脂肪酸
22. 解:(1)依题意,可设直线AB的方程为 ,代入抛物线方程
,代入抛物线方程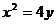 得
得
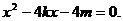 ①
①
设A、B两点的坐标分别是
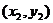 ,则
,则 、
、 是方程①的两根.
是方程①的两根.
所以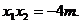
由点 分有向线段
分有向线段 所成的比为
所成的比为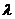 ,
,
 得
得 ,
即
,
即
又点Q是点P关于原点的以称点,
故点Q的坐标是 ,从而
,从而

=
 =
=
=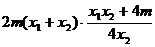 =
=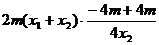 =0,所以
=0,所以 ………7分
………7分
(2) 由 得点A、B的坐标分别是(6,9)、(--4,4),
得点A、B的坐标分别是(6,9)、(--4,4),
由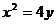 得
得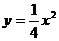 ,
,
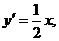
所以抛物线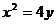 在点A处切线的斜率为
在点A处切线的斜率为 .
.
设圆 的方程是
的方程是 ,
,
则
解之得 
所以圆 的方程是
的方程是 .…………14分
.…………14分
21.解:①由题知 无解,所以
无解,所以 ,得
,得 .……4分
.……4分
②
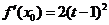 ,
,
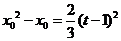 ,
,
设 ,原题即证
,原题即证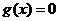 在
在 上必有解,并讨论解的个数.
上必有解,并讨论解的个数.

 ,
,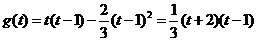 . …………6分
. …………6分
 1o当
1o当 或
或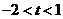 时,
时, ,
,
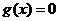 在
在 上必有解,且只有一解;
上必有解,且只有一解;
2o当 时,
时, 且
且 ,但
,但 ,
,
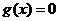 在
在 上有解,且有2个解;
上有解,且有2个解;
3o当 时,
时, ,
,
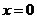 或
或 ,
,
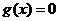 在
在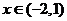 上有且只有一解,
上有且只有一解,
4o当 时,
时,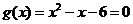 ,
,
 或
或 ,
,
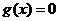 在
在 上有且只有一解,
上有且只有一解,
综上所述:对于任意的 ,总存在
,总存在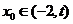 ,满足
,满足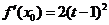 ,且当
,且当 或
或 时,有唯一解,当
时,有唯一解,当 时,有两个解. …………12分
时,有两个解. …………12分
20.解:① ,
, ,
,
两式相减,得 ,
, ,又
,又 ,
,
 数列
数列 为等比数列.
…………6分
为等比数列.
…………6分
②由①知 ,
, ,而
,而 ,
,
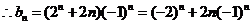 ,
,
当 时,
时,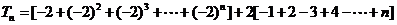
 ;
;
当 时,
时,

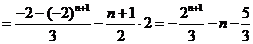 ,
,
综上所述: . …………12分
. …………12分
19. 解法一:(Ⅰ)取
解法一:(Ⅰ)取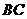 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
 正三棱柱
正三棱柱 中,平面
中,平面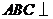 平面
平面 ,
,
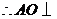 平面
平面 .
.
连结 ,在正方形
,在正方形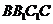 中,
中,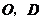 分别为
分别为
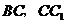 的中点,
的中点,
 ,
,
 .
.
在正方形 中,
中,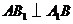 ,
,
 平面
平面 .
………………………4分
.
………………………4分
(Ⅱ)设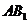 与
与 交于点
交于点 ,在平面
,在平面 中,作
中,作 于
于 ,连结
,连结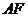 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面 .
.
 ,
,
 为二面角
为二面角 的平面角.
的平面角.
在 中,由等面积法可求得
中,由等面积法可求得 ,
,
又 ,
,
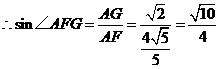 .
.
所以二面角 的大小为
的大小为 .……………………8分
.……………………8分
(Ⅲ)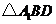 中,
中, ,
,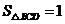 .
.
在正三棱柱中, 到平面
到平面 的距离为
的距离为 .
.
设点 到平面
到平面 的距离为
的距离为 .
.
由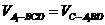 得
得 ,
,
 .
.
 点
点 到平面
到平面 的距离为
的距离为 .…………………………………12分
.…………………………………12分
解法二:(Ⅰ)取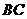 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
 在正三棱柱
在正三棱柱 中,平面
中,平面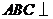 平面
平面 ,
,
 平面
平面 .
.
 取
取 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
,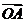 的方向为
的方向为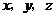 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
,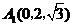 ,
, ,
, ,
,
 ,
, ,
, .
.
 ,
, ,
,
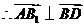 ,
, .
.
 平面
平面 .………………4分
.………………4分
(Ⅱ)设平面 的法向量为
的法向量为 .
.
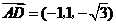 ,
, .
.
 ,
, ,
,

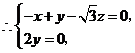

令 得
得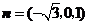 为平面
为平面 的一个法向量.
的一个法向量.
由(Ⅰ)知 平面
平面 ,
,
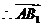 为平面
为平面 的法向量.
的法向量.
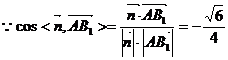
 二面角
二面角 的大小为
的大小为 .………………………………8分
.………………………………8分
(Ⅲ)由(Ⅱ), 为平面
为平面 法向量,
法向量,
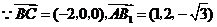 .
.
∴点 到平面
到平面 的距离
的距离 . …………12分
. …………12分
18.解:①记甲、乙、丙三位教师中恰有两位教师使用电脑的概率为P1,
则P1=
 +
+ 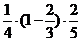 +
+ 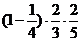 =
=  ;…………6分
;…………6分
②记此时电脑无法满足需求的概率为P2,
则P2=
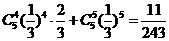 .…………12分
.…………12分
17.解:(Ⅰ) ,
,




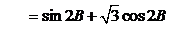
 …………4分
…………4分
又

 …………6分
…………6分
(2)由 ,
,
由正弦定理得: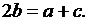
 ,
,
即
由余弦弦定理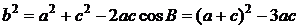 ,
,
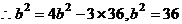 ,
, …………12分
…………12分
13.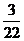 14.
14.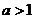 15.24 16.①②
15.24 16.①②
22. 如图,过抛物线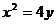 的对称轴上任一点
的对称轴上任一点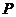

 作直线与抛物线交于
作直线与抛物线交于 两点,点
两点,点 是点
是点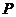 关于原点的对称点.
关于原点的对称点.
(1)设点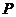 分有向线段
分有向线段 所成的比为λ,证明
所成的比为λ,证明 ;
;
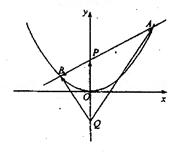 (2)设直线
(2)设直线 的方程是
的方程是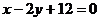 ,过
,过 两点的圆
两点的圆 与抛物线在点
与抛物线在点 处有共同的切线,
处有共同的切线,
求圆 的方程.
的方程.
高三数学试卷(文)答案及评分标准
21.已知函数 .
.
①若直线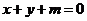 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围;
的取值范围;
②若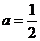 ,求证:对于任意的
,求证:对于任意的 ,总存在
,总存在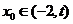 ,满足
,满足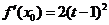 ,并确定这样的
,并确定这样的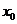 的个数.
的个数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com