
3. 在直角坐标系中,满足不等式
在直角坐标系中,满足不等式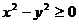 的点
的点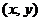 的集合是下面哪个图的阴影部分
的集合是下面哪个图的阴影部分
( )
2.设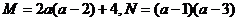 ,则
,则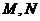 的大小关系为 ( )
的大小关系为 ( )
A.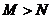 B.
B.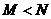 C.
C.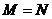 D.以上都有可能
D.以上都有可能
1.不等式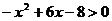 的解集为 ( )
的解集为 ( )
A. B.
B.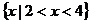
C.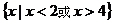 D.
D.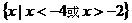
21. 解:(Ⅰ)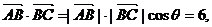 ①
①
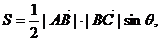 ②
②
②÷①得: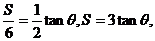 由
由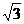 ≤S≤3,得
≤S≤3,得 -----2分
-----2分
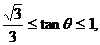 ∴
∴ 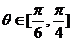 .--------------------------------------6分
.--------------------------------------6分
(Ⅱ)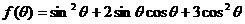 =2
=2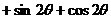
 (3)设M(x1,y1), N(x2,y2), Q(0,y0),
(3)设M(x1,y1), N(x2,y2), Q(0,y0), 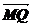 =(-x1,y0-y1),
=(-x1,y0-y1), 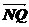 =(-x2,y0-y2)
=(-x2,y0-y2)
∵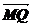 ∥
∥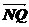 , ∴-x1(y0-y2)=-x2(y0-y1)
, ∴-x1(y0-y2)=-x2(y0-y1)
由y1=5x12, y2=5x22得y0=-5x1x2 ------------------------------------------9分
又∵∠MON为锐角,∴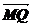 •
•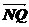 > 0 ,则x1x2+y1y2 > 0 --------11分
> 0 ,则x1x2+y1y2 > 0 --------11分
得 -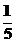 y0+25×(
y0+25×(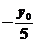 )2>0
, y0>
)2>0
, y0>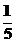 或y0<0 -----
--------------14分
或y0<0 -----
--------------14分
20. 解:由余弦定理得: 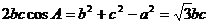 ,
-------------3分
,
-------------3分
 ,
,  ------------------6分
------------------6分
由正弦定理
得: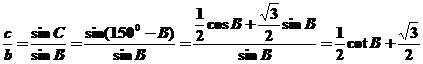 --10分
--10分
∵ 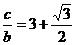 ∴
∴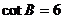 ,
, 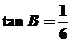 13分
13分
19. 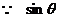 ,
, 为方程
为方程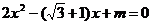 的两根
的两根
则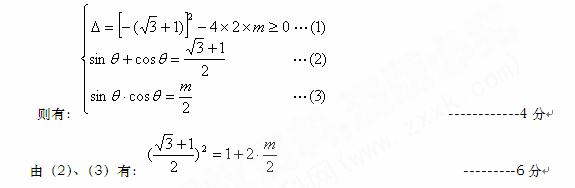 解得
解得 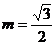 此时
此时
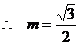
9分
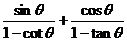 =
=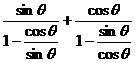 =
=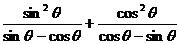
=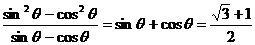 -----------------12分
-----------------12分
18.解: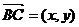
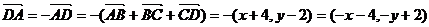
(1)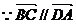 则有
则有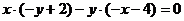
化简得: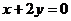 ----------------4分
----------------4分
(2)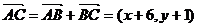
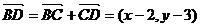
又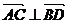 则
则 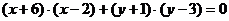 --------------6分
--------------6分
化简有: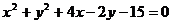
联立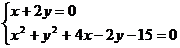 -----------9分
-----------9分
解得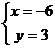 或
或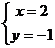 -----------12分
-----------12分
17. (1) 略---------------5分
(2)由y=sinx图象像右移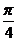 个单位后, 再保持纵坐标不变, 横坐标缩为原来的
个单位后, 再保持纵坐标不变, 横坐标缩为原来的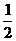 , 最后横坐标不变, 纵坐标伸长到原来的2倍, 便得到y=f(x)的图象.---------------5分
, 最后横坐标不变, 纵坐标伸长到原来的2倍, 便得到y=f(x)的图象.---------------5分
15.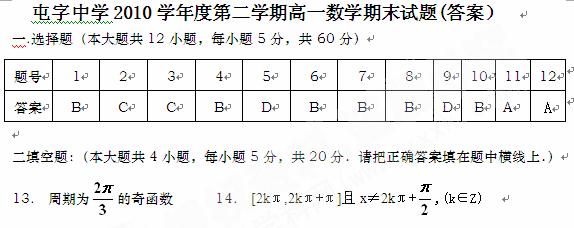 3,
3,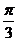 16. 三点为A、B、D
16. 三点为A、B、D
22.(14分)已知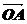 =(2,1),
=(2,1),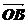 = (1,7),
= (1,7),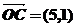 ,若
,若 =
=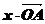 ,
,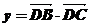
(x,y∈R)
(1) 求y=f(x)的解析式.
(2) 求y=f(x)的图象按向量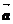 =(-2,8)平移后得到的图象y=g(x)解析式,
=(-2,8)平移后得到的图象y=g(x)解析式,
(3) 过原点O作OM,ON分别交于y=g(x)的图象于M,N两点,直线MN
交y轴于点Q(0, y0),当∠MON为锐角时,求y0的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com