1． 如果正比例函数及反比例函数图象都经过点（-2，4），则正比例函数的解析式为              ，反比例函数的解析式为                  ．

4.探究性问题的解题思路没有固定的模式和套路，解答相关问题时，可从以下几个角度考虑：（1）特殊点法；（2）分类讨论法；（3）类比猜测法等，最重要的还是要结合具体题目的特点进行分析，灵活选择和运用适当的数学思想及解题技巧。

●拓展演练

3.利用转化思想，通过求点的坐标，来达到求线段长度；通过求线段的长度求点的坐标；通过一元二次方程根的判别式及根与系数的关系来解决抛物线与x轴交点问题。

2.应用函数性质解决相关问题时，要树立数形结合思想，借助函数的图象和性质，形象、直观地解决有关不等式、最值、方程的解、以及图形的位置关系等问题。

1.正确理解和掌握各种函数的概念、图象和性质，这是解决所有函数问题的基本前提。

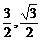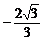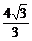【答案】（1）B；（2）y=x²+x；（3）存在点C坐标为()，此时四边形ABCO的面积最大为。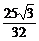

【方法点拨】（1）解题方法较为灵活，容易解决。（2）因为已具备图象上三点坐标，可直接设为一般式，代入三点求解；也可以设为两根式，再代入点B坐标求解。（3）关键要抓住四边形ABCO的面积由两部分组成，其中△OAB面积为定值，因此要四边形面积最大，问题转化为判断△OBC面积是否存在最大值。

●难点突破方法总结

函数在中考中占有很重要的地位，是中考必考内容之一。课改实验区的函数综合题其背景材料更加丰富，更加贴近生活，更加注重对解决问题的思维过程的考查，但其计算量和书写量与非课改区相比，又有较大幅度的下降。在完成函数问题方面，要注重以下几点。

此时，点C坐标为()，四边形ABCO的面积为.

∴ 当x=时，△OBC面积最大，最大面积为.

∴ S_△OBC= .

而 |CF|==，