
23.(本题满分10分)
(Ⅰ)直线的直角坐标方程为: ;
;
………………3分
(Ⅱ)原点到直线的距离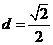 ,
,
直线参数方程为: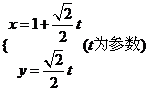 曲线
曲线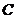 的直角坐标方程为:
的直角坐标方程为: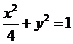 ,
,
联立得: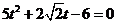 ,求得
,求得
所以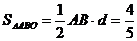 …………………………10分
…………………………10分
2高.考.资.源+网4高.考.资.源+网.(本题满分10分)
令 ,
,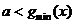 即可
即可
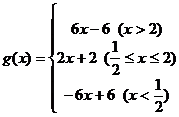 ,当
,当 时,
时, 取最小值3
取最小值3
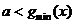 即可, 故
即可, 故 .
…………………………………10分
.
…………………………………10分
22.(本题高.考.资.源+网满分10分)
(Ⅰ) 证明:

 ∽
∽
∴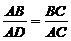 ,即
,即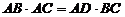 ……………………4分
……………………4分
(Ⅱ) 由射影定理知
由射影定理知
又由三角形相似可知 ,且
,且
∴ ,结合射影定理
,结合射影定理
∴ …………
………… 分
分
21. (本题满分12分)
(Ⅰ)由 在抛物线
在抛物线 上可得,
上可得, ,抛物线方程为
,抛物线方程为 ………1分
………1分
设抛物线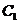 的切线方程为:
的切线方程为:
联立,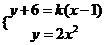 ,由
,由 ,可得
,可得
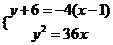 可知
可知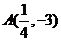
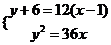 可知
可知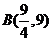 ……………………3分
……………………3分
易求直线 方程为
方程为 ………………………4分
………………………4分
弦 长为
长为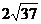 ……………………5分
……………………5分
(Ⅱ)设 ,三个点都在抛物线
,三个点都在抛物线 上,故有
上,故有
 ,作差整理得
,作差整理得
 ,
,
所以直线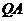 :
: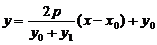 ,直线
,直线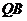 :
: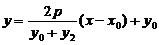
…………………6分
因为 均是抛物线
均是抛物线 的切线,故与抛物线
的切线,故与抛物线 方程联立,
方程联立,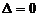 ,可得:
,可得:
 ,
,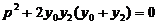
两式相减整理得: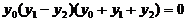 ,即可知
,即可知
……………………8分
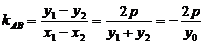
所以直线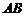 :
: ,与抛物线
,与抛物线 联立消去
联立消去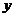
得关于 的一元二次方程:
的一元二次方程: ……………………10分
……………………10分
易知其判别式
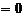 ,因而直线
,因而直线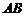 与抛物线
与抛物线 相切.故直线
相切.故直线 与抛物线
与抛物线 相切.
相切.
…………………………………………12分
20.(本题满分12分)
(Ⅰ) 设
设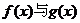 交于点
交于点 ,则有
,则有
 ,即
,即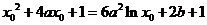
 (1)
(1)
又由题意知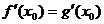 ,即
,即 (2) ……2分
(2) ……2分
由(2)解得
将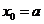 代入(1)整理得
代入(1)整理得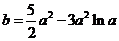 …………………………4分
…………………………4分
令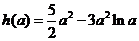 ,则
,则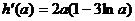
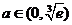 时,
时, 递增,
递增,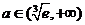 时
时 递减,所以
递减,所以
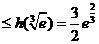
即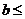
 ,
, 的最大值为
的最大值为 ……………………………………6分
……………………………………6分
(Ⅱ)不妨设 ,
,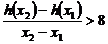 变形得
变形得
令 ,
,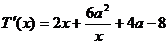 ,
,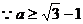 ,高.考.资.源+网
,高.考.资.源+网

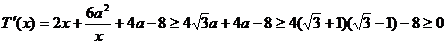
 在
在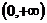 内单调增,
内单调增,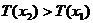 ,同理可证
,同理可证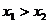 命题成立
命题成立
……………………12分
19.(本题满分高.考.资.源+网12分)
解:(Ⅰ)众数:4.6和4.7;中位数:4.75 …………………………2分
(Ⅱ)设 表示所取3人中有
表示所取3人中有 个人是“好视力”,至多有1人是“好视力”记为事件
个人是“好视力”,至多有1人是“好视力”记为事件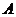 ,则
,则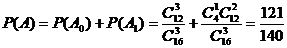 ……………6分
……………6分
(Ⅲ)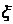 的可能取值为0、1、2、3高.考.资.源+网
…………………7分高.考.资.源+网
的可能取值为0、1、2、3高.考.资.源+网
…………………7分高.考.资.源+网
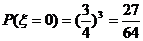
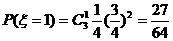
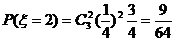
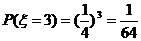
分布列为
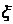

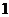
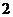
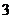

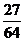
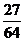
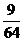

………………………10分
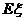
 .
……………………12分
.
……………………12分
18.(本题满分高.考.资.源+网12分)
解:(Ⅰ)连接 ,不妨设
,不妨设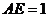 ,则
,则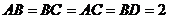 ,于是
,于是
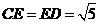 ,
,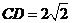 ,所以
,所以 ,
, ,
,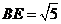 …………… 3分
…………… 3分
所以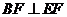 ,又
,又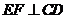 ,又
,又 为两条相交直线
为两条相交直线
故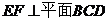 ……………………………………6分
……………………………………6分
(Ⅱ)由(Ⅰ)可知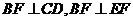 ,所以
,所以 面
面
又过 作
作 ,交
,交 于点
于点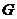 ,连接
,连接
因此 为二面角
为二面角 的平面角
……………………9分
的平面角
……………………9分
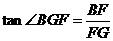 ,而
,而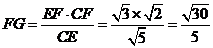
所以 ………………………………12分
………………………………12分
17.(本题满分12分)
解:(Ⅰ)因为 ,所以
,所以 …………………………2分
…………………………2分
又因为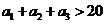 ,所以
,所以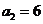 ,故公比
,故公比 …………4分
…………4分
所以 ………………………6分
………………………6分
(Ⅱ)设 公差为
公差为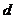 ,所以
,所以 …………………8分
…………………8分
由 ,可知
,可知 ,
, ……………………10分
……………………10分
所以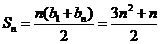 ……………………
……………………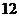 分
分
13.  14.
14.
 15.
15.  16.
16. 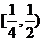
24.(本小题满分10分)选修4-5:不等式选讲
若关于 的不等式
的不等式 恒成立,求
恒成立,求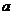 的取值范围.
的取值范围.
2010年四校联考第二次高考模拟考试
数学试卷(理工类)评分标准
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线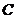 的参数方程为
的参数方程为 (
(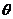 为参数).
为参数).
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线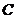 交于
交于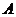 ,
, 四两点,原点为
四两点,原点为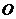 ,求
,求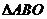 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com