
(二)主要方法:
1.对映射有两个关键点:一是有象,二是象惟一,缺一不可;
2.对函数三要素及其之间的关系给以深刻理解,这是处理函数问题的关键;
3.理解函数和映射的关系,函数式和方程式的关系.
(一)主要知识:
1.对应、映射、像和原像、一一映射的定义;
2.函数的传统定义和近代定义;
3.函数的三要素及表示法.
22、(13分)袋子A和B中分别装有若干个质地均匀大小相同的红球和白球,从A中摸出一个球,得到红球的概率是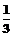 ,从B中摸出一个球,得到红球的概率是P.
,从B中摸出一个球,得到红球的概率是P.
(1)若A、B两个袋子中的球数之比为1:3,将A、B中的球混装在一起后,从中摸出一个球得到红球的概率是 ,求P的值;
,求P的值;


(2)从A中有放回地摸球,每次摸出一个,若累计3次摸到红球即停止,最多摸球5次,5次之内(含5次)不论是否有3次摸到红球都停止摸球;记5次之内(含5次)摸到红球的次数为随机变量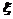 ,求随机变量
,求随机变量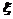 的分布列及数学期望.
的分布列及数学期望.
21、 (13分)20、如图,在正四棱锥
(13分)20、如图,在正四棱锥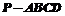 中,E是侧棱PB的中点,侧棱PA与底面ABCD所成角的正切值为
中,E是侧棱PB的中点,侧棱PA与底面ABCD所成角的正切值为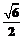 .
.


(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)求异面直线PD与AE所成角的正切值;
(3)在侧面PAD上寻找一点F,使EF⊥侧面PBC,试确定点F的位置,并证明你找出的点F满足EF⊥侧面PBC.
20、(12分)甲、乙、丙三人参加了一家公司招聘面试,甲表示只要面试合格就签约,乙、丙则约定两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合格互不影响.
,且面试是否合格互不影响.
(1)求甲、乙、丙三人中至少有一人面试合格的概率;


(2)求签约人数的分布列和方差.
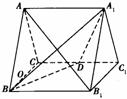
19、(12分)如图,正三棱柱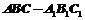 的所有棱长都为2,D为
的所有棱长都为2,D为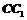 中点.
中点.
(1)求证: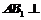 平面
平面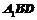 ;
;
(2)求二面角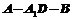 的大小;
的大小;


(3)求点C到平面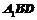 的距离.
的距离.
18、(12分)(1)甲、乙、丙、丁四名同学排成一排,分别计算下列条件的排法种数(写出表达式并计算出结果). 


①甲不在排头,乙不在排尾;
②甲一定在乙右端.
(2)8个人分配到4辆车上工作,每车两人,按下列要求有多少种不同的分配方法?(写出表达式).
①若车不相同,车上工种不同;
②若车相同,车上工种相同. 


17、(12分)(1)在四面体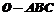 中,
中,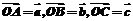 ,D为BC的中点,E为AD的中点,用
,D为BC的中点,E为AD的中点,用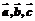 表示出
表示出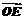 .
.
(2)已知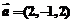 ,
,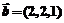 ,求以
,求以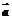 、
、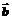 为邻边的平行四边形的面积.
为邻边的平行四边形的面积. 


16、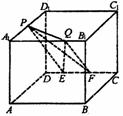 在边长为1的正方体
在边长为1的正方体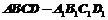 中,P为
中,P为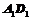 的中点,Q为
的中点,Q为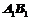 上任意一点,E、F为CD上任意两点,且EF的长为定值,考虑下面四个量:
上任意一点,E、F为CD上任意两点,且EF的长为定值,考虑下面四个量:
①点P到平面QEF的距离;②直线PQ与平面PEF所成角
③二面角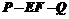 的大小 ;④三棱锥
的大小 ;④三棱锥 的体积.
的体积.
其中是常量的有 .
15、若多项式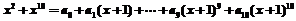 ,则
,则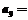 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com