
20.甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止。设甲在每局中获胜的概率为p(p>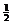 ),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为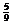 .
.
(1)求p的值;
(2)设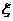 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量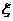 的分布列和数学期望E
的分布列和数学期望E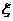
19.已知数列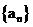 满足
满足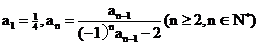
(1)求证:数列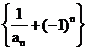 (
(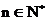 )是等比数列;
)是等比数列;
(2)设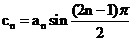 ,数列
,数列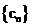 的前n项和
的前n项和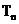 ,求证:对任意的
,求证:对任意的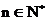 ,
, 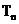
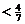
18.已知正三棱柱ABC-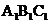 的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱C
的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱C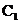 上的点,且CN=2
上的点,且CN=2
(1)求二面角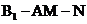 的平面角的余弦值;
的平面角的余弦值;
(2) 求点 到平面AMN的距离;
到平面AMN的距离;
21.(12分)是否存在锐角 和
和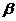 ,使得①
,使得①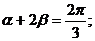 ②
②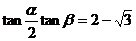
同时成立?若存在,求出 和
和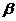 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

20.(12分)已知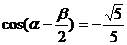 ,
,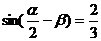 ,且
,且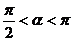 ,
,
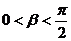 ,求
,求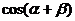 的值.
的值.
19.(12分)已知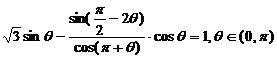 求
求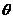 的值;
的值;
18.(13分)已知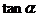 、
、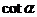 是关于
是关于 的方程
的方程 的两个实根,
的两个实根,
且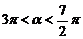 ,求
,求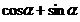 的值.
的值.
17.(13分) 求证: 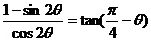
过程或演算步骤。
16.(13分)(1)已知角 终边上一点P(-4,3),求
终边上一点P(-4,3),求 的值.
的值.
(2)已知 ,求
,求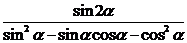 的值.
的值.
15.已知数列 满足
满足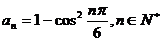 ,则它的前2010项的和是
;
,则它的前2010项的和是
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com