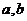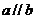3．已知向量，则“”是“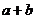=0”的　　 (　　 )

　　 A．充分不必要条件　　　 B．必要不充分条件

　　 C．充分必要条件　　 D．既不充分也不必要条件

2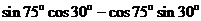．的值为　　　　　 (　　 )

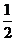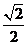　　 A．1　　 B．　 C． D．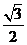

1．在复平面内，复数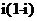(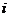是虚数单位)对应的点位于　　 (　　 )

　　 A．第一象限 B．第二象限 C．第三象限 D．第四象限

24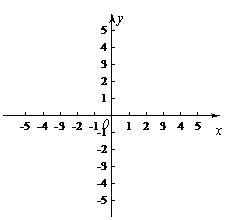．(本题满分12分)

如图，在平面直角坐标系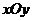中，抛物线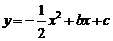

经过点，．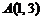

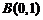(1)求抛物线的表达式及其顶点坐标；

(2)过点A作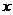轴的平行线交抛物线于另一点C，

①求△ABC的面积；

②在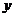轴上取一点P，使△ABP与△ABC相似，

求满足条件的所有P点坐标．

数学课上，张老师出示了问题1：

如图25-1，四边形ABCD是正方形， BC =1，对角线交点记作O，点E是边BC延长线上一点．联结OE交CD边于F，设，，求关于的函数解析式及其定义域．

(1)经过思考，小明认为可以通过添加辅助线--过点O作OM⊥BC，垂足为M求解．你认为这个想法可行吗？请写出问题1的答案及相应的推导过程；

(2)如果将问题1中的条件“四边形ABCD是正方形，BC =1”改为“四边形ABCD是平行四边形，BC=3，CD=2，”其余条件不变(如图25-2)，请直接写出条件改变后的函数解析式；

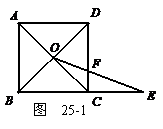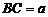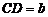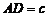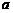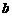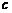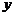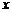(3)如果将问题1中的条件“四边形ABCD是正方形，BC =1”进一步改为：“四边形ABCD是梯形，AD∥BC，，，(其中，，为常量)”其余条件不变(如图25-3)，请你写出条件再次改变后关于的函数解析式以及相应的推导过程．

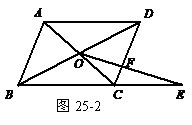
23．(本题满分12分)

如图，正方形ABCD中，E是AD边上一点，且BE=CE，

BE与对角线AC交于点F，联结DF，交EC于点G．

(1)求证：∠ABF =∠ADF；

(2)求证：DF⊥EC．

22．(本题满分10分)

某中学对九年级准备选考1分钟跳绳的同学进行测试，测试结果如下表：

　　　　　　频数分布表

组别	跳绳(次/1分钟)	频数
第1组	190~199	5
第2组	180~189	11
第3组	170~179	23
第4组	160~169	33
第5组	150~159	8

(1)此次测试成绩的中位数落在第　▲　组中；

(2)如果成绩达到或超过180次/分钟的同学可获满分，那么本次测试中获得满分的人数占参加测试人数的　▲　%；

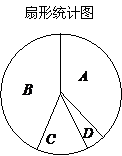
(3)如果该校九年级参加体育测试的总人数为200人，若要绘制一张统计该校各项目选考人数分布的扇形图(如22题图)，图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比，那么该扇形的圆心角应为　▲　°；

(4)如果此次测试的平均成绩为171次/分钟，那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平？为什么？

21．(本题满分10分)

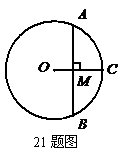如图，已知OC是⊙O的半径，弦AB＝6，AB⊥OC，垂足为M，且CM＝2．

(1)联结AC，求∠CAM的正弦值；

(2)求OC的长．

20．(本题满分10分)解方程：．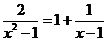

19．(本题满分10分)

解不等式组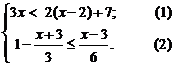：，并把它的解集表示在数轴上．

18．在⊙O中，若弦AB是圆内接正四边形的边，弦AC是圆内接正六边形的边，则∠BAC=　▲　　．