
17. (本题满分16分)
执行流程图所示算法,可得到数列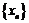 . 其中
. 其中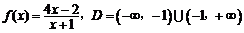 .
.
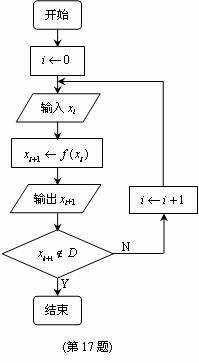 (1)要使输出的结果是一个无穷的常数列,求应输入的初始数据x0的值;
(1)要使输出的结果是一个无穷的常数列,求应输入的初始数据x0的值;
(2)若输出的数列有且只有3项,请写出该数列的所有项;
(3)若输入x0时,产生的无穷数列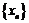 满足:
满足: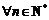 ,均有
,均有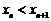 ,求x0的取值范围.
,求x0的取值范围.
16. (本题满分14分)
已知集合A,B满足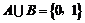 ,试分别用分类计数原理、分步计数原理求出A,B的组数.
,试分别用分类计数原理、分步计数原理求出A,B的组数.
15. (本题为选做题,满分28分. 请在A、B、C三题中选做两题,并在答题纸相应区域作答. 若三题均选做,则按前两题计分)
A.(选修4-1:几何证明选讲)
如图,D是线段AB的一个三等分点,以D为圆心,AD为半径作圆D,自B引圆D的切线,切点为E,点C是BE延长线上的动点,且线段CA与圆D交于点F. 求证:∠CFE为定值.
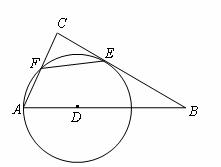
B.(选修4-2:矩阵与变换)
在直角坐标系中,已知点A(1,2)和B(3,-1)在一个二阶矩阵M的作用下,变换所得到的点分别是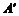 (4,5)和
(4,5)和 (5,1). 求矩阵M.
(5,1). 求矩阵M.
C.(选修4-4:坐标系与参数方程)
在平面直角坐标系xOy中,以O为极点,Ox为极轴建立极坐标系,且两种坐标系长度单位一致. 已知曲线C的极坐标方程为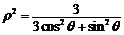 ,曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.
,曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.
14. 设a1,b1,c1,a2,b2,c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为M和N. 那么“ ”是“M=N”的 ▲ 条件(在“充要”、“充分不必要”、“必要不充分”、“既非充分又非必要”中选一个填写).
”是“M=N”的 ▲ 条件(在“充要”、“充分不必要”、“必要不充分”、“既非充分又非必要”中选一个填写).
13. 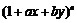 (常数a,b
(常数a,b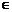 Z,
Z,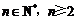 )展开式中不含x的项的系数的绝对值之和为729,不含y的项的系数的绝对值之和为64,则共可组成 ▲ 对有序数对(a,b).
)展开式中不含x的项的系数的绝对值之和为729,不含y的项的系数的绝对值之和为64,则共可组成 ▲ 对有序数对(a,b).
12. 有甲、乙、丙、丁四位同学参加数学竞赛,其中只有一位同学获奖. 有人走访了四位同学,甲说:“丙获奖了”. 乙说:“我获奖了”. 丙说:“乙、丁都未获奖”. 丁说:“是乙或丙获奖了”. 四位同学的话中,恰有两句是对的,则获奖的同学是 ▲ .
11. 关于复数(i为虚数单位),有下列四个命题:
①若 ,则
,则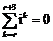 ;
;
②复数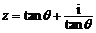 在复平面上对应的点不可能在实轴和虚轴上;
在复平面上对应的点不可能在实轴和虚轴上;
③“复数 ”的充要条件是“
”的充要条件是“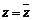 ”;
”;
④设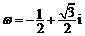 ,则
,则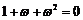 .
.
其中,真命题的序号是 ▲ .
10. 某一批花生种子,如果每1粒发芽的概率是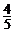 ,那么播下4粒恰有2粒发芽的概率是 ▲.
,那么播下4粒恰有2粒发芽的概率是 ▲.
9. 南非世界杯足球赛第一阶段是小组赛,采用小组内单循环比赛形式(即组内任意两队之间比赛1场)已知参赛的32支球队平均分成8个小组,则小组赛总共要进行 ▲ 场比赛.
8. 已知随机事件M,N,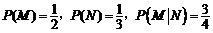 ,则
,则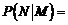 ▲ .
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com