
6.
 已知
已知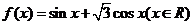 ,函数
,函数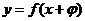 的图象关于直线
的图象关于直线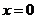 对称,则
对称,则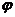 的值可以是
的值可以是
A.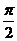 B.
B.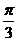 C.
C.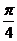 D.
D.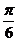
5. 、
、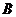 、
、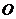 是平面内不共线的三个定点,且
是平面内不共线的三个定点,且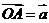 ,
,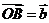 ,点
,点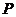 关于点
关于点 的对称点为
的对称点为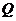 ,点
,点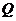 关于点
关于点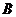 的对称点为
的对称点为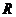 ,则点
,则点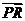 等于
等于
A.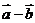 B.
B.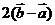 C.
C.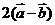 D.
D.
4. 是定义在
是定义在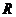 上的偶函数,且在
上的偶函数,且在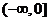 上为增函数,若
上为增函数,若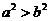 ,则以下结论正确的是
,则以下结论正确的是
A. B.
B.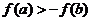 C.
C.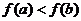 D.
D.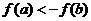
3.一个工厂生产了某种产品27000件,它们来自甲、乙、丙3条生产线.现采用分层抽样的方法,对这批产品进行抽样测试,已知从甲、乙、丙3条生产线依次抽取的产品件数恰好组成一个等差数列,则这批产品中乙生产线生产的产品数量是
A.13500 B.9000 C.3000 D.6000
2.若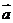 与
与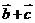 都是非零向量,则“
都是非零向量,则“ ”是“
”是“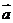 ∥
∥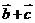 ”的
”的
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
1.若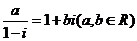 ,则复数
,则复数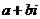 =
=
A.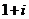 B.
B.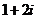 C.
C. D.
D.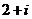
21.在各项均为正数的数列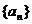 中,前
中,前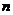 项和
项和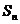 满足
满足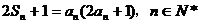 。
。
(1)证明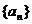 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前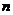 项和的公式;
项和的公式;
(2)在平面直角坐标系 面上,设点
面上,设点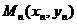 满足
满足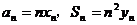 ,且点
,且点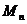 在直线
在直线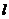 上,
上,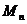 中最高点为
中最高点为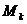 ,若称直线
,若称直线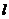 与
与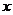 轴、直线
轴、直线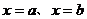 所围成的图形的面积为直线
所围成的图形的面积为直线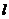 在区间
在区间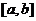 上的面积,试求直线
上的面积,试求直线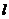 在区间
在区间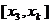 上的面积;
上的面积;
(3)若存在圆心在直线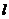 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列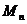 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.
20.在以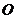 为原点的直角坐标系中,点
为原点的直角坐标系中,点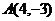 为
为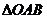 的直角顶点,若
的直角顶点,若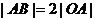 ,且点
,且点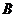 的纵坐标大于0
的纵坐标大于0
(1)求向量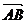 的坐标;
的坐标;
(2)是否存在实数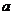 ,使得抛物线
,使得抛物线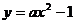 上总有关于直线
上总有关于直线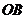 对称的两个点?若存在,求实数
对称的两个点?若存在,求实数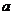 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
19.若函数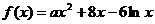 在点
在点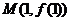 处的切线方程为
处的切线方程为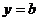
(1)求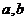 的值;
的值;
(2)求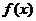 的单调递增区间;
的单调递增区间;
(3)若对于任意的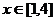 ,恒有
,恒有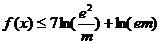 成立,求实数
成立,求实数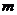 的取值范围(其中e为自然对数的底数).
的取值范围(其中e为自然对数的底数).
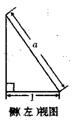
18.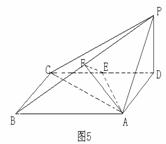 如图5,四棱锥
如图5,四棱锥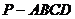 中,底面
中,底面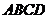 为矩形,
为矩形,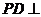 底面
底面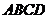 ,
,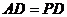 ,
,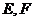 分别为
分别为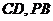 的中点
的中点
(1)求证: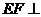 面
面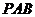 ;
;
(2)若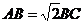 ,求
,求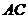 与面
与面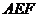 所成角的余弦值.
所成角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com