

第一节 语法和词汇知识(共15小题,每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21. By the year 1889, there were just 541 bison in the whole of North America.
A. leaving alive B. to leave alive C. to be left alive D. left alive
22.解:(1) ∵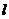 是线段A
是线段A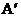 的中垂线,∴
的中垂线,∴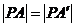 ,
,
∴||PA|-|P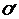 ||=||P
||=||P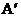 |-|P
|-|P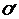 ||=|
||=|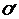
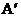 |=
|=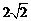 .
.
即点P在以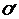 、A为焦点,以4为焦距,以
、A为焦点,以4为焦距,以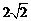 为实轴长的双曲线上,
为实轴长的双曲线上,
故轨迹C的方程为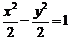 .
………6分
.
………6分
(2)设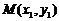 ,
,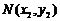 ,则直线
,则直线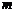 的方程为
的方程为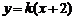 ,则由
,则由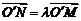 ,得
,得
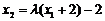 ,
,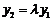 .由
.由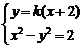 ,得
,得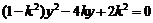 .
.
 ∴
∴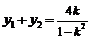 ,
,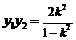 ,
, .
.
由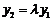 ,
,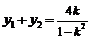 ,
,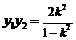 ,消去
,消去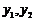 ,得
,得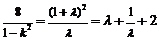 .
.
∵ ,函数
,函数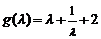 在
在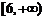 上单调递增.
上单调递增.
∴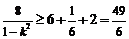 ,
,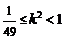 ,所以
,所以
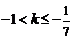 或
或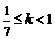
故直线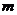 的斜率
的斜率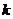 的取值范围为
的取值范围为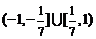 . ………14分
. ………14分
20. 解:(1)当
解:(1)当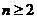 时,
时,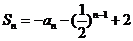 ,
,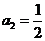
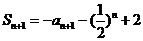
所以
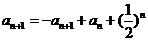 ,
即
,
即 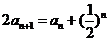 ……2分
……2分
所以
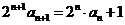 即
即 ,
,
 ……3分
……3分
又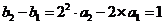 ……4分 (没有这一步骤扣1分)
……4分 (没有这一步骤扣1分)
所以,
 ,
,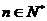 即
即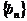 为等差数列 ……5分
为等差数列 ……5分
(2)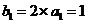
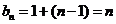 ∴
∴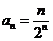 ……7分
……7分
(3)由于 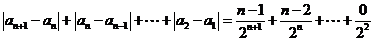 ………8分
………8分
令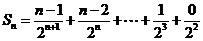
则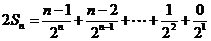 ………9分
………9分
两式相减,得:

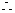
 或
或 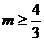
又 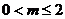
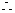
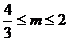 ------------12分
------------12分
19.解:作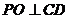 于
于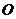 ,连接
,连接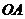
由侧面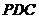 与底面
与底面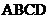 垂直,则
垂直,则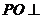 面
面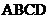
所以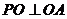 且
且 ,
,
又由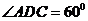 ,
,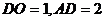 ,
,
则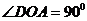 ,即
,即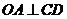 ……………2分
……………2分
分别以OA,OC,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,
18. 解:(1)三人中恰好有两人选择QQ音乐的概率为P=
解:(1)三人中恰好有两人选择QQ音乐的概率为P=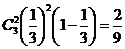 ………6分
………6分
(2)记第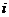 名用户选择的应用属于农场、音乐、读书分别为事件
名用户选择的应用属于农场、音乐、读书分别为事件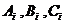 ,i=1,2,3.由题意知
,i=1,2,3.由题意知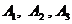 相互独立,
相互独立,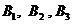 相互独立,
相互独立,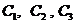 相互独立,
相互独立,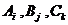 (i,j,k=1,2,3且i,j,k互不相同)相互独立,且
(i,j,k=1,2,3且i,j,k互不相同)相互独立,且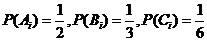 .
.
他们选择的应用互不相同的概率为
 …………12分
…………12分
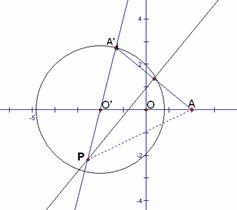
22. 如图,已知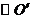 :
: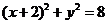 及点
及点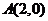 ,在
,在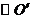 上任取一点
上任取一点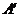 ,连
,连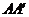 并作
并作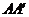 的中垂线
的中垂线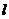 ,设
,设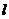 与直线
与直线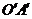 交于点
交于点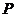 ,若点
,若点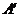 取遍⊙
取遍⊙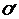 上的点.
上的点.
(1)求点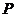 的轨迹
的轨迹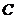 的方程;
的方程;
 (2)若过点
(2)若过点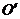 的直线
的直线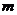 与曲线
与曲线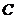 交于
交于 两点,且
两点,且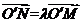 ,则当
,则当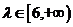 时,求直线
时,求直线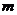 的斜率
的斜率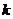 的取值范围.
的取值范围.
21.已知函数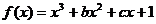 在区间
在区间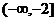 上是增函数,在区间
上是增函数,在区间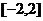 上是减函数,且
上是减函数,且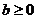 .
.
(Ⅰ)求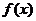 的表达式;
的表达式;
(Ⅱ)设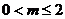 ,若对任意的
,若对任意的 ,不等式
,不等式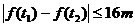 恒成立,求实数
恒成立,求实数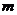 的最小值.
的最小值.
20.已知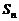 是数列
是数列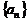 的前n项和,
的前n项和,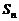 满足关系式
满足关系式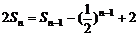 ,
,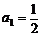
(n≥2,n为正整数).
(1)令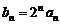 ,证明:数列
,证明:数列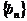 是等差数列;
是等差数列;
(2)求数列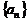 的通项公式;
的通项公式;
(3)对于数列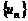 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的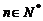 ,恒有
,恒有
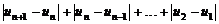 ≤M成立,称数列
≤M成立,称数列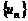 为“差绝对和有界数列”,
为“差绝对和有界数列”,
证明:数列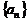 为“差绝对和有界数列”.
为“差绝对和有界数列”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com