
22. (本题满分12分)
解:(1)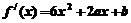 ,由题意可知,x=-1,x=2是方程6x2+2ax+b=0的两根,故:x1+x2==
,由题意可知,x=-1,x=2是方程6x2+2ax+b=0的两根,故:x1+x2== 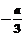 =1, ∴a=-3,-2=
=1, ∴a=-3,-2=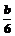 , ∴b=-12, 又,当x=-1时f(x)的极值是8,
, ∴b=-12, 又,当x=-1时f(x)的极值是8,
∴c=1 ∴f(x)=2x3-3x2-12x+1 (6分)
(2)∵f(x)=6x2-6x-12, 令f(x)=0, 即6x2-6x-12=0, ∴x=2或x=-1,
解得函数的单调区间为:
增区间为:(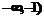 ,(2,
,(2,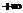 ) 单调减区间为(-1,2)
(6分)
) 单调减区间为(-1,2)
(6分)
21、(本题满分12分)解: P:0<c<1,﹃P:c≥1
Q: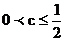 ,
﹃Q:
,
﹃Q: 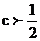
P或Q为真, P且Q为假,则P和Q中只有一个正确。
由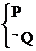 或
或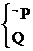 得
得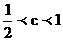 或c≥1
或c≥1
20.(本题满分12分)解: (1)销售单价每增加1元,日均销售量减少40桶。设在进价基础上增加x元后,日均销售利润为y元,这时日均销售量P=480-40(x-1)=520-40x (0<x<13)
(2)y=(520-40x)x-200=-40x2+520x-200 (0<x<13)
易知,当x=6.5时,y有最大值。即这个经营部每桶定价11.5元才能获得最大利润。
19. (本题满分12分)解:(1)由 f(-1)=0得a-b+1=0
又因为对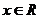 恒有
恒有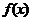
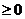 ,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,
,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,
所以a=1 b=2 得 f(x)=x2+2x+1
(2)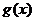 =
=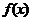 -kx= x2+(2-k)x+1是单调函数,则
-kx= x2+(2-k)x+1是单调函数,则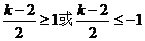 ,
,
所以得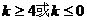
18.(本小题满分12分)
解:(1)设f(x)=ax2+bx+c,则f(0)=c=1.f(x+1)-f(x)=a(x+1)2+b(x+1)-ax2-bx=2x,即
2ax+a+b=2x 所以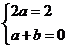 得
得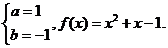
(2)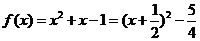 ,x∈
,x∈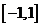
x=1时fmax=1, x=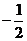 时fmin=
时fmin=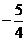 ,
,
17.(本题满分10分)
解:(Ⅰ)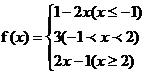
(Ⅱ)x<-2或x>3
fmin=3
22.(本题满分12分)
已知f(x)=2x3+ax2+bx+c在x=-1处取得极值8,又x=2时,f(x) 也取得极值。
(1)求a,b,c的值,写出f(x)的解析式;
(2)求f(x)的单调区间。
高二数学期末试题(文)答题卡 选择填空题:(16×5=80分)
21.(本题满分12分)
已知c>0.设命题P:函数y=cx在R上单调递减;Q: 函数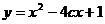 在
在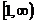 上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。
上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。
20.(本题满分12分)
某桶装水经营部每天的房租,人员工资等固定成本为200元,每桶水的进价是5元。销售单价与日均销售的关系如下表所示
|
销售单价(元) |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
日均销售量(桶) |
480 |
440 |
400 |
360 |
320 |
280 |
240 |
设在进价基础上增加x元后,日均销售利润为y元。请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
19.(本题满分12分)
函数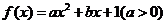
(1)若f(-1)=0,并对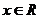 恒有
恒有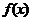
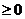 ,求
,求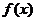 的表达式;
的表达式;
(2)在(1)的条件下,对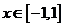 ,
,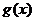 =
=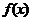 -kx是单调函数,求k的范围。
-kx是单调函数,求k的范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com