

(四)巩固练习:
1.函数 的值域为
的值域为 .
.
2.若函数 在
在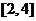 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则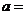
 .
.
(二)(配方法) ,
,
∴ 的值域为
的值域为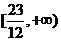 .
.
改题:求函数 ,
,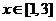 的值域.
的值域.
解:(利用函数的单调性)函数 在
在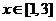 上单调增,
上单调增,
∴当 时,原函数有最小值为
时,原函数有最小值为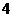 ;当
;当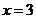 时,原函数有最大值为
时,原函数有最大值为 .
.
∴函数 ,
,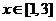 的值域为
的值域为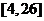 .
.
(2)求复合函数的值域:设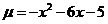 (
(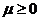 ),则原函数可化为
),则原函数可化为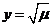 .
.
又∵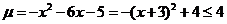 ,∴
,∴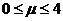 ,故
,故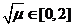 ,
,
∴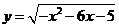 的值域为
的值域为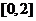 .
.
(3)(法一)反函数法: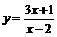 的反函数为
的反函数为 ,其定义域为
,其定义域为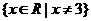 ,
,
∴原函数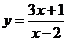 的值域为
的值域为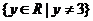 .
.
(法二)分离变量法: ,
,
∵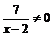 ,∴
,∴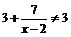 ,
,
∴函数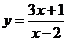 的值域为
的值域为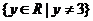 .
.
(4)换元法(代数换元法):设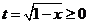 ,则
,则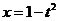 ,
,
∴原函数可化为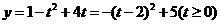 ,∴
,∴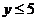 ,
,
∴原函数值域为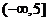 .
.
说明:总结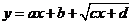 型值域,变形:
型值域,变形: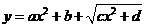 或
或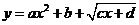
(5)三角换元法:∵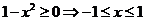 ,∴设
,∴设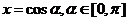 ,
,
则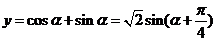
∵ ,∴
,∴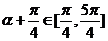 ,∴
,∴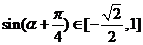 ,
,
∴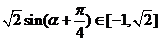 ,
,
∴原函数的值域为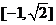 .
.
(6)数形结合法: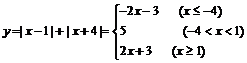 ,∴
,∴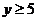 ,
,
∴函数值域为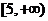 .
.
(7)判别式法:∵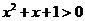 恒成立,∴函数的定义域为
恒成立,∴函数的定义域为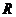 .
.
由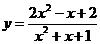 得:
得: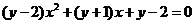 ①
①
①当 即
即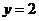 时,①即
时,①即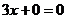 ,∴
,∴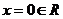
②当 即
即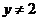 时,∵
时,∵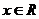 时方程
时方程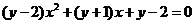 恒有实根,
恒有实根,
∴ ,
, ∴
∴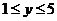 且
且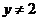 ,
,
∴原函数的值域为 .
.
(8) ,
,
∵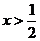 ,∴
,∴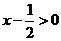 ,∴
,∴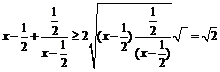 ,当且仅当
,当且仅当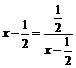 时,即
时,即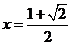 时等号成立.∴
时等号成立.∴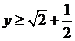 ,∴原函数的值域为
,∴原函数的值域为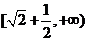 .
.
(9)(法一)方程法:原函数可化为: ,
,
∴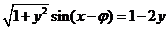 (其中
(其中 ),
),
∴ ,∴
,∴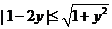 ,∴
,∴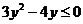 ,∴
,∴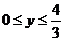 ,
,
∴原函数的值域为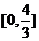 .
.
(法二)数形结合法:可看作求点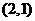 与圆
与圆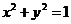 上的点的连线的斜率的范围,解略.
上的点的连线的斜率的范围,解略.
例2.若关于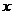 的方程
的方程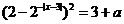 有实数根,求实数
有实数根,求实数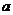 的取值范围.
的取值范围.
解:原方程可化为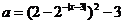 ,
,
令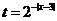 ,则
,则 ,
,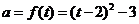 ,又∵
,又∵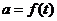 在区间
在区间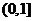 上是减函数,
上是减函数,
∴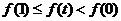 ,即
,即 ,
,
故实数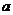 的取值范围为:
的取值范围为: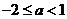 .
.
例3.(《高考 计划》考点9,智能训练16)某化妆品生产企业为了占有更多的市场份额,拟在2003年度进行一系列的促销活动.经过市场调查和测算,化妆品的年销量
计划》考点9,智能训练16)某化妆品生产企业为了占有更多的市场份额,拟在2003年度进行一系列的促销活动.经过市场调查和测算,化妆品的年销量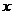 万件与年促销费用
万件与年促销费用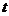 万元
万元 之间满足:
之间满足: 与
与 成反比例;如果不搞促销活动,化妆品的年销量只能是1万件.
成反比例;如果不搞促销活动,化妆品的年销量只能是1万件.
已知2003年,生产化妆品的固定投入为3万元,每生产1万件化妆品需再投入32万元.当将每件化妆品的售价定为“年平均每件成本的150%”与“年平均每件所占促销费的一半”之和,则当年产销量相等.
(1)将2003年的年利润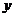 万元表示为年促销费
万元表示为年促销费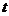 万元的函数;
万元的函数;
(2)该企业2003年的促销费投入多少万元时,企业的年利润最大?
(注:利润=收入-生产成本-促销费)
解:(1)由题设知: ,且
,且 时,
时, ,∴
,∴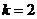 ,即
,即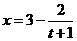 ,
,
∴年生产成本为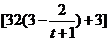 万元,年收入为
万元,年收入为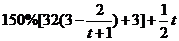 .
.
∴年利润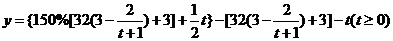 ,
,
∴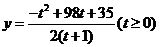 .
.
(2)由(1)得
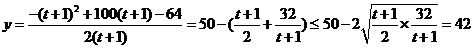 ,
,
当且仅当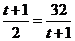 ,即
,即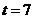 时,
时,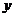 有最大值
有最大值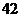 .
.
∴当促销费定为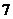 万元时,
万元时,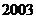 年该化妆品企业获得最大利润.
年该化妆品企业获得最大利润.
(三)例题分析:
例1.求下列函数的值域:
(1) ; (2)
; (2)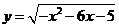 ; (3)
; (3)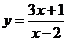 ;
;
(4) ; (5)
; (5)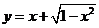 ; (6)
; (6)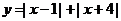 ;
;
(7)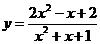 ; (8)
; (8)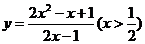 ; (9)
; (9)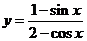
解:(1)(一)公式法(略)
(二)主要方法(范例分析以后由学生归纳):
求函数的值域的方法常用的有:直接法,配方法,判别式法,基本不等式法,逆求法(反函数法),换元法,图像法,利用函数的单调性、奇偶性求函数的值域等.
(一)主要知识:
1.函数的值域的定义;2.确定函数的值域的原则;3.求函数的值域的方法.
24、第三次科技革命推动了国际经济格局的调整,主要反映在
A、为改变国际经济旧秩序创造了条件
B、美欧经济差距缩小


C、增强了发展中国家的经济实力
D、进一步扩大了发达国家与发展中国家的经济差距

 2009-2010(下)巴中市四县中期末联考高2011级
2009-2010(下)巴中市四县中期末联考高2011级
历史试题
第Ⅰ卷 选择题(共48分)
第Ⅱ卷 非选择题
23、2008年9月以来,美国次贷危机引发的金融危机愈演愈烈,各国股市受到重创,巨幅下跌,冰岛、巴基斯坦濒临国家破产,金融海啸席卷全球,由此引发了人们对全球化的再思考。对此思考正确的是


A、在这场全球性的金融危机中,发达国家受到的损失最大
B、发展中国家处于完全不利地位,面临最大的经济风险
C、为了维护本国金融安全,不要对发达国家开放金融市场
D、发展中国家应该尽可能减少对发达国家的金融依赖程度
22、“金砖四国”指巴西、俄罗斯、印度和中国。巴西被称为“世界原料基地”,俄罗斯被称为“世界加油站”,印度被称为“世界办公室”,中国被称为“世界工厂”。你认为印度被称为“世界办公室”的主要原因是
A、科学技术方面取得令人瞩目的成就 B、建立起比较齐全的工业体系
C、实现了粮食的基本自给 D、成为了世界军事强国。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com