
19.(本小题满分12分)
设函数
(I)
若对任意的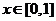 ,不等式
,不等式 都成立,求实数
都成立,求实数 的最小值;
的最小值;
(II)
求函数 在区间
在区间 上的极值。
上的极值。
18.(本小题满分12分)
 已知四棱锥P-ABCD的三视图如右图。该棱锥中,
已知四棱锥P-ABCD的三视图如右图。该棱锥中,
PA=AB=1,PD与平面ABCD所成角是30°,点
F是PB的中点,点E在棱BC上移动。
(I)画出该棱锥的直观图并证明:无论点E在棱
BC的何处,总有 ;
;
(II)当BE等于何值时,二面角P-DE-A的大小为
45°。
17.(本小题满分12分)
甲、乙等5名世博会志愿者同时被随机地安排到A、B、C、D四个不同的岗位服务,每个岗位至少有1名志愿者。
(I)求甲、乙两人同时参加A岗位服务的概率;
(II)求甲、乙两人不在同一个岗位服务的概率;
(III)设随机变量 为这5名志愿者中参加A岗位服务的人数,求
为这5名志愿者中参加A岗位服务的人数,求 的分布和数学期望
的分布和数学期望 。
。
16.(本小题满分12分)
已知向量 ,向量
,向量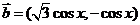 ,函数
,函数 。
。
(I)
求函数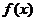 的最小正周期;
的最小正周期;
(II)
求函数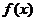 的单调递增区间;
的单调递增区间;
(III)
求函数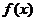 在区间
在区间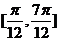 上的值域。
上的值域。
15.若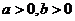 ,且
,且 则
则 的最大值是
的最大值是
14.给出下列四个结论:
①命题 的否定是
的否定是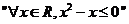
②“若 ,则
,则 ”的逆命题为真;
”的逆命题为真;
③已知直线 ,则
,则 的充要条件是
的充要条件是 ;
;
④对于任意实数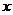 ,有
,有 且
且 时,
时, ,
, ,则
,则 时,
时, 。
。
其中正确结论的序号是 (填上所有正确结论的序号)
13.已知直线 的极坐标方程为
的极坐标方程为 ,圆M的参数方程为
,圆M的参数方程为
 (
( 为参数),则圆M上的点到直线
为参数),则圆M上的点到直线 的最短距离为 。
的最短距离为 。
12.一个口袋中装有4个红球和6个白球,这些球除颜色外完全相同,一次从中摸出4个球,至少摸到2个红球的概率为 。
11.在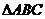 中,
中, 、
、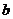 、
、 分别是角A、B、C所对的边,
分别是角A、B、C所对的边, ,则
,则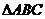
的面积S= 。
10.已知 、
、 是三次函数
是三次函数 的两个极值点,且
的两个极值点,且 ,
,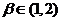 ,则
,则 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
第II卷(非选择题,共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com