
5.平面内有三点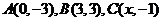 ,且
,且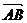 ∥
∥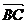 ,则
,则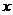 的值是( )
的值是( )
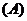 1
1 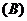 5
5 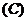
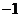
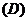
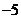
4.在三角形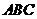 中,已知
中,已知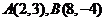 ,点
,点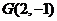 在中线
在中线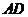 上,且
上,且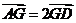 ,则点
,则点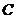 的坐标是
( )
的坐标是
( )
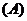
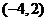
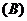
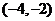
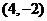
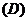
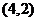
3.已知向量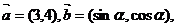 且
且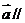
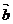 ,则
,则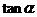 = ( )
= ( )
(A)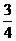 (B)
(B)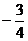 (C)
(C)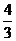 (D)
(D)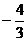
2.已知平面上直线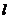 的方向向量
的方向向量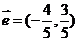 ,点
,点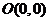 和
和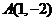 在
在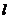 上的射影分别是
上的射影分别是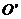 和
和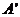 ,则
,则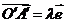 ,其中
,其中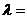 ( )
( )
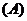
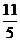
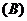
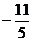
 2
2  -2
-2
1.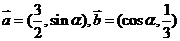 且
且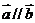 ,则锐角
,则锐角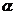 为
( )
为
( )
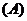
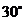
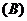
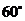
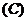

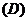
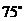
(四)例题分析:
例1.已知向量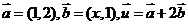 ,
,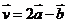 ,且
,且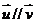 ,求实数
,求实数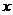 的值。
的值。
解:因为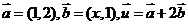 ,
,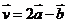
所以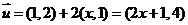 ,
,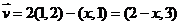
又因为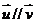
所以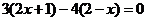 ,即
,即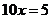
解得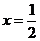
例2.已知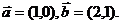
(1)求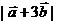 ;
(2)当
;
(2)当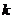 为何实数时,
为何实数时,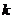
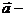
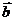 与
与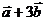 平行,
平行时它们是同向还是反向?.
平行,
平行时它们是同向还是反向?.
解:(1)因为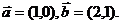
所以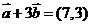
则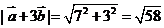
(2)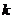
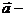
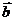
 ,
,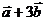
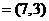
因为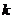
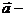
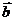 与
与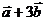 平行
平行
所以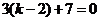 即得
即得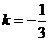
此时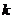
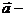
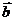
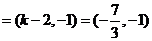 ,
,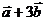
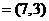
则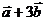
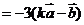 ,即此时向量
,即此时向量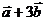 与
与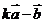 方向相反。
方向相反。
例3.已知点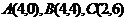 ,试用向量方法求直线
,试用向量方法求直线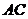 和
和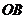 (
(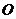 为坐标原点)交点
为坐标原点)交点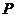 的坐标.
的坐标.
解:设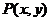 ,则
,则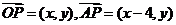
因为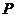 是
是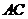 与
与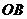 的交点
的交点
所以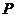 在直线
在直线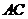 上,也在直线
上,也在直线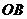 上
上
即得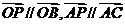
由点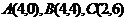 得,
得,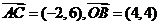
得方程组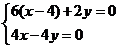 ,解之得
,解之得
故直线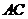 与
与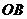 的交点
的交点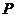 的坐标为
的坐标为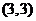 。
。
例4.已知点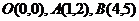 及
及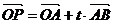 ,试问:
,试问:
(1)当 为何值时,
为何值时,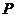 在
在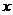 轴上?
轴上? 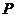 在
在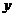 轴上?
轴上? 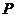 在第三象限?
在第三象限?
(2)四边形 是否能成为平行四边形?若能,则求出
是否能成为平行四边形?若能,则求出 的值.若不能,说明理由.
的值.若不能,说明理由.
解:(1)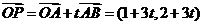 ,则
,则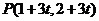
若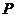 在
在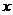 轴上,则
轴上,则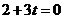 ,所以
,所以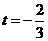 ;
;
若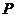 在
在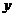 轴上,则
轴上,则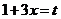 ,所以
,所以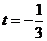 ;
;
若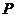 在第三象限,则
在第三象限,则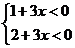 ,所以
,所以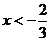 。
。
(2)因为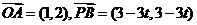
若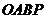 是平行四边形,则
是平行四边形,则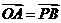 ,所以
,所以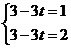 此方程组五解;
此方程组五解;
故四边形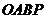 不可能是平行四边形。
不可能是平行四边形。
(三)基础训练:
1.若向量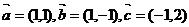 ,则
,则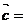 ( )
( )
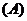
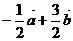
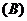
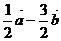
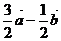
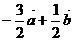
2.设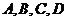 四点坐标依次是
四点坐标依次是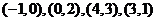 ,则四边形
,则四边形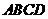 为( )
为( )
 正方形
正方形  矩形
矩形
 菱形
菱形
 平行四边形
平行四边形
3.下列各组向量,共线的是 ( )
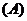
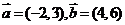
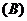
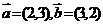
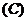
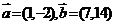
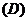
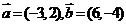
4.已知点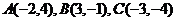 ,且有
,且有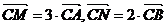 ,则
,则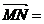 .
.
5.已知点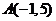 和向量
和向量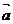 =
=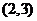 ,若
,若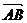 =3
=3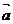 ,则点B的坐标为 。
,则点B的坐标为 。
6.设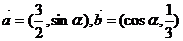 ,且有
,且有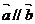 ,则锐角
,则锐角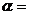 。
。
(二)主要方法:
1.建立坐标系解决问题(数形结合);
2.向量位置关系与平面几何量位置关系的区别;
3.认清向量的方向求坐标值得注意的问题;
(一)主要知识:
1.平面向量坐标的概念;
2.用向量的坐标表示向量加法、减法、数乘运算和平行等等;
3.会利用向量坐标的定义求向量的坐标或点的坐标及动点的轨迹问题.
2.学会使用分类讨论、函数与方程思想解决有关问题..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com