
4、设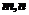 是两条不同的直线,
是两条不同的直线,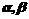 是两个不同的平面,考查下列命题,其中正确的命题是
是两个不同的平面,考查下列命题,其中正确的命题是
A、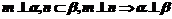 B、
B、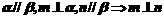
C、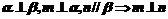 D、
D、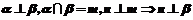
3、某篮球运动员在三分线投球的命中率为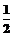 ,他投球10次,恰好投进3个球的概率为
,他投球10次,恰好投进3个球的概率为
A、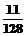 B、
B、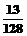 C、
C、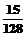 D、
D、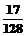
2、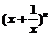 展开式的二项式系数之和为64,则展开式的常数项为
展开式的二项式系数之和为64,则展开式的常数项为
A、10 B、20 C、30 D、120
1、已知向量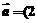 、
、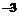 、
、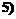 ,
,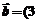 、
、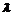 、
、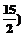 ,且
,且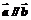 ,则
,则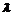 等于
等于
A、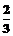 B、
B、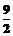 C、
C、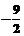 D、
D、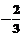
22、甲、乙两人各射击一次,击中目标的概率分别是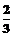 和
和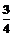 ,假设两人射击是否击中目标,相互之间没有影响,每次射击是否击中目标,相互之间没有影响.
,假设两人射击是否击中目标,相互之间没有影响,每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击,问乙恰好射击5次后,被中止射击的概率是多少?
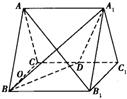
21、(12分)如图,正三棱柱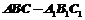 的所有棱长都为2,D为
的所有棱长都为2,D为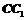 中点.
中点.
(1)求证: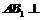 平面
平面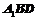 ;
;
(2)求二面角 的大小;
的大小;
(3)求点C到平面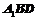 的距离.
的距离.
20、(12分)甲、乙、丙三人参加了一家公司招聘面试,甲表示只要面试合格就签约,乙、丙则约定两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是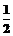 ,且面试是否合格互不影响.
,且面试是否合格互不影响.
(1)求甲、乙、丙三人中至少有一人面试合格的概率;
(2)求签约人数为1人的概率.
18、(12分)(1)甲、乙、丙、丁四名同学排成一排,分别计算下列条件的排法种数(写出表达式并计算出结果).
①甲不在排头,乙不在排尾;
②甲一定在乙右端.
(2)8个人分配到4辆车上工作,每车两人,按下列要求有多少种不同的分配方法?(写出表达式).
①若车不相同,车上工种不同;
②若车相同,车上工种相同.
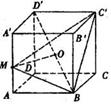 19(12分)、已知正方体
19(12分)、已知正方体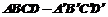 的棱长为1,点M是棱
的棱长为1,点M是棱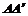 的中点,点O是对角线
的中点,点O是对角线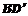 的中点.
的中点.
(1)求证:OM是异面直线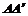 和
和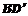 的公垂线;
的公垂线;
(2)求二面角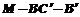 的大小;
的大小;
(3)求三棱锥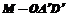 的体积.
的体积.
17、(12分)(1)在四面体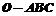 中,
中, ,D为BC的中点,E为AD的中点,用
,D为BC的中点,E为AD的中点,用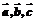 表示出
表示出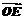 .
.
(2)已知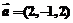 ,
,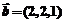 ,求以
,求以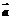 、
、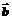 为邻边的平行四边形的面积.
为邻边的平行四边形的面积.
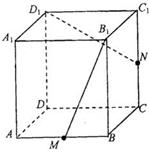
16、如图所示,在正方体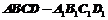 中,M、N分别是棱AB、
中,M、N分别是棱AB、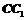 的中点,
的中点,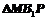 的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
①平面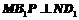 ;②平面
;②平面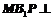 平面
平面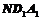 ;③
;③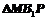 在底面ABCD上的射影图形的面积为定值;④
在底面ABCD上的射影图形的面积为定值;④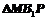 在侧面
在侧面 上的射影图形是三角形.
上的射影图形是三角形.
其中正确命题的序号是
. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com