
19.(本小题满分13分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动。若厂家投放A、B型号电视机的价值分别为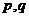 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为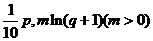 万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元(精确到
万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元(精确到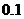 ,参考数据:
,参考数据: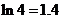 )
)
(1)当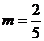 时,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
时,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况。
18.(本小题满分12分)
如图,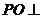 平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC
平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC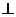 AB,BC=CD=BO=PO,
AB,BC=CD=BO=PO,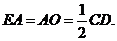
(1)求证:PE 平面PBC;
平面PBC;
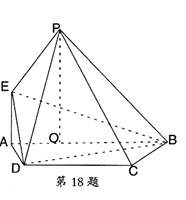 (2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
(2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
17.(本小题满分12分)
某市卫生部防疫部门为了控制某种病毒的传染,提供了批号分别为1,2,3,4,5的五批疫苗,供全市所辖的A、B|C三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种。
(1)求三个区注射的疫苗批号互不相同概率;
(2)记A、B、C三个区选择的疫苗批号最大数为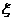 ,求
,求 的期望。
的期望。
16.(本小题满分12分)
已知向量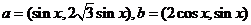 ,定义
,定义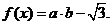
(I)求函数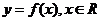 的单调递减区间;
的单调递减区间;
(II)若函数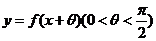 为偶函数,求
为偶函数,求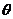 的值。
的值。
15.三条直线两两异面,则称为一组“T型线”,任选正方体12条面对角线中的三条,“T型线”的组数为 。
14.抛物线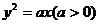 与直线
与直线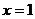 围成的封闭图形的面积为
围成的封闭图形的面积为 ,若直线
,若直线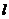 与抛物线相切且平行于直线
与抛物线相切且平行于直线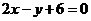 ,则
,则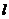 的方程为 。
的方程为 。
13.已知下列命题:
①已知 表示两个不同的平面,
表示两个不同的平面,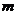 为平面
为平面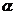 内的一条直线,则“
内的一条直线,则“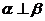 ”是“
”是“ ”的充要条件;
”的充要条件;
②函数 图象对称中心的坐标为
图象对称中心的坐标为 ;
;
③在平面直角坐标系中圆C的方程为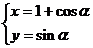 (
(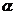 为参数),若以原点为极点,
为参数),若以原点为极点,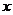 轴非负半轴为极轴,则圆C的极坐标方程为
轴非负半轴为极轴,则圆C的极坐标方程为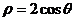 ;
;
④在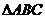 中,若
中,若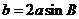 (其中
(其中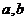 分别为
分别为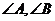 的对边),则A等于30°,
的对边),则A等于30°,
其中真命题的序号是 (填上所有正确的序号)。
12.已知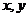 满足不等式组
满足不等式组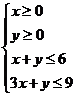 ,则
,则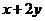 的最大值是
。
的最大值是
。
11.函数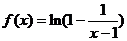 的定义域是
。
的定义域是
。
10.已右函数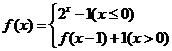 ,把函数
,把函数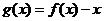 的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为 ( )
的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为 ( )
A.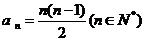 B.
B.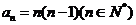
C.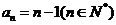 D.
D.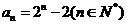
第Ⅱ卷(满分100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com