
1.线段的定比分点:内分点、外分点、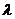 的确定;
的确定;
2.掌握平移公式,会用平移公式化简函数式或求平移后的函数解析式.
1.掌握线段的定比分点坐标公式和中点坐标公式,会用定比分点坐标公式求分点坐标和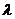 ,会用中点坐标公式解决对称问题;
,会用中点坐标公式解决对称问题;
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.设 ,则
,则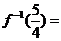 .
.
2.设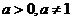 ,函数
,函数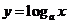 的反函数和
的反函数和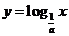 的反函数的图象关于( )
的反函数的图象关于( )
 轴对称
轴对称
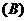
 轴对称
轴对称 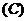
 轴对称
轴对称 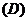 原点对称
原点对称
3.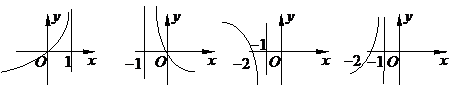 已知函数
已知函数 ,则
,则 的图象只可能是
(
)
的图象只可能是
(
)
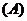
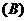
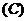
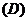
4.若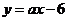 与
与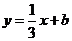 的图象关于直线
的图象关于直线 对称,且点
对称,且点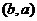 在指数函数
在指数函数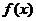 的图象上,则
的图象上,则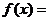 .
.
(三)例题分析:
例1.求下列函数的反函数:
(1)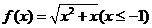 ;(2)
;(2)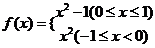 ;
;
(3)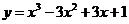 .
.
解:(1)由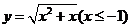 得
得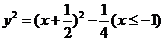 ,
,
∴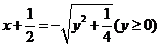 ,
,
∴所求函数的反函数为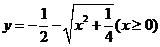 .
.
(2)当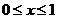 时,得
时,得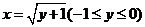 ,当
,当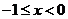 时,
时,
得 ,
,
∴所求函数的反函数为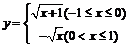 .
.
(3)由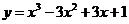 得
得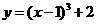 ,∴
,∴ ,
,
∴所求反函数为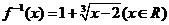 .
.
例2.函数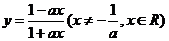 的图象关于
的图象关于 对称,求
对称,求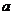 的值.
的值.
解:由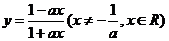 得
得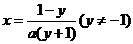 ,
,
∴ ,
,
由题知: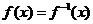 ,
,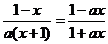 ,∴
,∴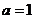 .
.
例3.若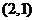 既在
既在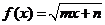 的图象上,又在它反函数图象上,求
的图象上,又在它反函数图象上,求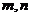 的值.
的值.
解:∵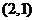 既在
既在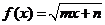 的图象上,又在它反函数图象上,
的图象上,又在它反函数图象上,
∴ ,∴
,∴ ,∴
,∴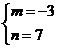 .
.
例4.(《高考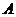 计划》考点12“智能训练第5题”)设函数
计划》考点12“智能训练第5题”)设函数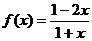 ,又函数
,又函数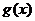 与
与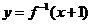 的图象关于
的图象关于 对称,求
对称,求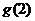 的值.
的值.
解法一:由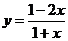 得
得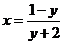 ,∴
,∴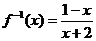 ,
,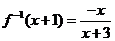 ,
,
∴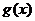 与
与 互为反函数,由
互为反函数,由 ,得
,得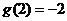 .
.
解法二:由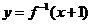 得
得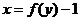 ,∴
,∴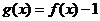 ,
,
∴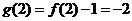 .
.
例5.已知函数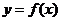 (定义域为
(定义域为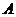 、值域为
、值域为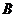 )有反函数
)有反函数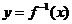 ,则方程
,则方程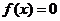 有解
有解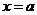 ,且
,且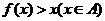 的充要条件是
的充要条件是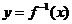 满足
满足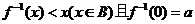 .
.
例6.(《高考 计划》考点12“智能训练第15题”)已知
计划》考点12“智能训练第15题”)已知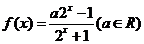 ,是
,是 上的奇函数.(1)求
上的奇函数.(1)求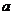 的值,(2)求
的值,(2)求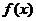 的反函数,(3)对任意的
的反函数,(3)对任意的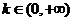 解不等式
解不等式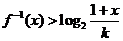 .
.
解:(1)由题知 ,得
,得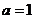 ,此时
,此时
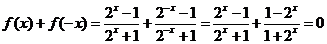 ,
,
即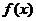 为奇函数.
为奇函数.
(2)∵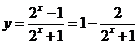 ,得
,得 ,
,
∴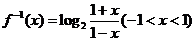 .
.
(3)∵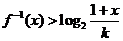 ,∴
,∴ ,∴
,∴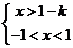 ,
,
①当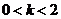 时,原不等式的解集
时,原不等式的解集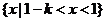 ,
,
②当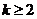 时,原不等式的解集
时,原不等式的解集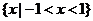 .
.
(二)主要方法:
1.求反函数的一般方法:(1)由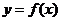 解出
解出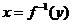 ,(2)将
,(2)将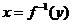 中的
中的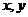 互换位置,得
互换位置,得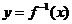 ,(3)求
,(3)求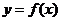 的值域得
的值域得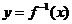 的定义域.
的定义域.
(一)主要知识:
1.反函数存在的条件:从定义域到值域上的一一映射确定的函数才有反函数;
2.反函数的定义域、值域上分别是原函数的值域、定义域,若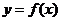 与
与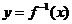 互为反函数,
互为反函数,
函数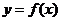 的定义域为
的定义域为 、值域为
、值域为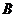 ,则
,则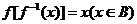 ,
,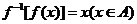 ;
;
3.互为反函数的两个函数具有相同的单调性,它们的图象关于 对称.
对称.
17.在横线处各补上一句话。要求:语意连贯,句式一致,形成完整的排比句。(6分)
人要懂得尊重别人,尊重别人所以不傲慢,不傲慢所以有德行;人要懂得尊重自己, , ;人要懂得尊重自然, , 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com