
21、解:(Ⅰ)首先,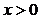 .
.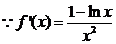 ,
1分
,
1分
 在
在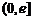 上递增;
上递增;
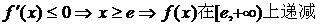 ;
;
 的单调递增区间是
的单调递增区间是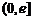 ,单调递减区间是
,单调递减区间是 . 3分
. 3分
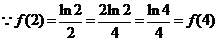 ,而
,而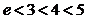 ,
,
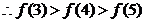 即
即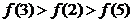 .
5分
.
5分
(Ⅱ)要证明 即证明
即证明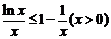 即证明
即证明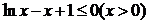 恒成立。
恒成立。
令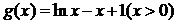 ,则
,则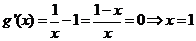 .
7分
.
7分
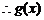 在
在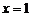 处取得极大值
处取得极大值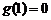 ,也是最大值。
,也是最大值。
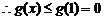 。
。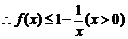 成立.
成立.
由此可得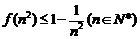 .
9分
.
9分
于是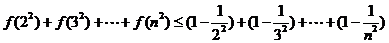
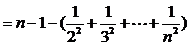
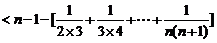
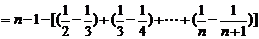

18、解:解:设指针落在A,B,C区域分别记为事件A,B,C.
则 .
.
(Ⅰ)若返券金额不低于30元,则指针落在A或B区域.

即消费128元的顾客,返券金额不低于30元的概率是 . 5分
. 5分
(Ⅱ)由题意得,该顾客可转动转盘2次.
所以随机变量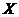 的可能值为0,30,60,90,120. 6分
的可能值为0,30,60,90,120. 6分

 设
设 ,
,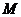 在
在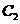 上,因为
上,因为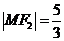 ,所以
,所以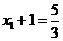 ,
,
得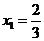 ,
, .
3分
.
3分
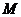 在
在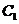 上,且椭圆
上,且椭圆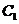 的半焦距
的半焦距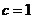 ,于是
,于是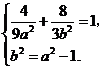 5分
5分
消去 并
并 整理得
整理得 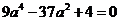 ,
解得
,
解得 (
( 不合题意,舍去).
不合题意,舍去).
故椭圆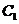 的方程为
的方程为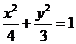 .
6分
.
6分
(Ⅱ)由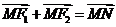 知四边形
知四边形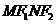 是平行四边形,其中心为坐标原点
是平行四边形,其中心为坐标原点 ,
,
因为 ,所以
,所以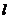 与
与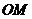 的斜率相同,
的斜率相同,
故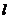 的斜率
的斜率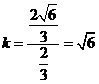 .
7分
.
7分
设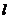 的方程为
的方程为 .
.
由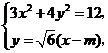
消去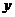 并化简得
并化简得 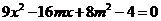 .
.
设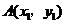 ,
,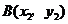 ,
,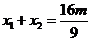 ,
,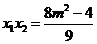 8分
8分

因为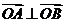 ,所以
,所以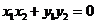 .
.
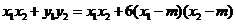
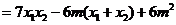
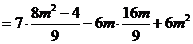
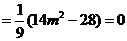 . 10分
. 10分
所以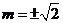 .此时
.此时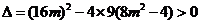 ,
,
故所求直线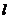 的方程为
的方程为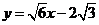 ,或
,或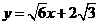 .
12分
.
12分
22、(本小题满分14分) 已知数列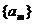 是首项为
是首项为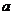 ,公差为
,公差为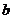 的等差数列,
的等差数列,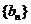 是首项为
是首项为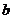 ,公比为
,公比为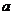 的等比数列,且满足
的等比数列,且满足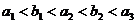 ,其中
,其中 .
.
(Ⅰ)求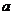 的值;
的值;
(Ⅱ)若数列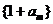 与数列
与数列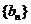 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列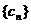 ,求数列
,求数列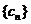 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列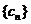 的前n项之和为
的前n项之和为 ,求证:
,求证:
 .
.

21、(本小题满分12分) ) 已知函数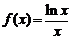 。
。
(Ⅰ)求函数 的单调区间,并比较
的单调区间,并比较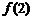 、
、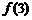 、
、 的大小;
的大小;
(II)证明: 在其定义域内恒成立,并比较
在其定义域内恒成立,并比较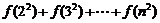 与
与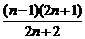 的大小。
的大小。
20、(本小题满分12分) 在直角坐标系xOy中,椭圆C1: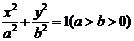 的左
的左 、右焦点分别为F1、F2.其中F2也是抛物线C2:
、右焦点分别为F1、F2.其中F2也是抛物线C2: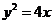 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且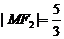 .
.
(1)求C1的方程;
(2)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若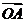 ·
·
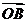 =0,求直线l的方程.
=0,求直线l的方程.
19、(本小题满分12分) 如 图所示,棱柱
图所示,棱柱 的所有棱长都等于2,
的所有棱长都等于2,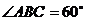 ,平面AA1C1C⊥ABCD,∠A1AC=60°.
,平面AA1C1C⊥ABCD,∠A1AC=60°.
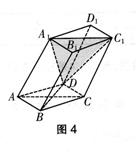 (I)证明:BD⊥AA1.
(I)证明:BD⊥AA1.
(II)求二面角D―A1A―C的平面角的余弦值.
(III)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,试说明理由.
18、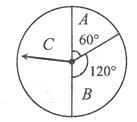 (本小题满分12分) 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(本小题满分12分) 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(I)若某位顾客消费128元 ,求返券金额不低于30元的概率;
,求返券金额不低于30元的概率;
(II)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为X(元).求随机变量X的分布列和数学期望。
17、(本小题满分12分) 在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,已知向量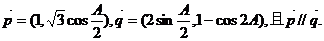
(I)若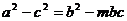 ,求实数m的值。
,求实数m的值。
(II)若 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
16、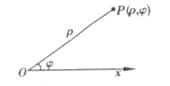 在平面上取定一点
在平面上取定一点 ,从
,从 出发引一条射线
出发引一条射线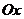 ,再取定一个长度单位及计算角的正方向,合称为一个极坐标系。这样,平面上任一点
,再取定一个长度单位及计算角的正方向,合称为一个极坐标系。这样,平面上任一点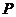 的位置就可以用线段
的位置就可以用线段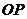 的长度
的长度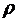 以及从
以及从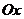 到
到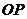 的角度
的角度
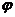 来确定,有序数对
来确定,有序数对 称为
称为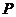 点的极坐标,
点的极坐标,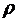 称为
称为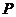 点的极径,
点的极径,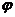 称为
称为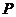 点的极角。在一个极坐标系下,给出下列命题:
点的极角。在一个极坐标系下,给出下列命题:


A.点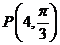 的极径为4,极角为
的极径为4,极角为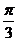 ;B
;B .有序数对
.有序数对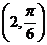 与
与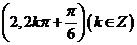 表示两个不同点;C.点
表示两个不同点;C.点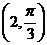 关于极点的对称点为
关于极点的对称点为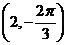 D.圆心在
D.圆心在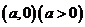 ,半径
,半径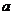 的圆的极坐标方程为
的圆的极坐标方程为 ;E.过点
;E.过点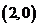 垂直极轴的直线方程为
垂直极轴的直线方程为 .其中真命题序号是
.
.其中真命题序号是
. 
15、在△ABC中,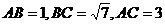 ,若O为△ABC的垂心,则
,若O为△ABC的垂心,则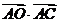 的值为 .
的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com