
4.在区间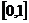 内任取三个数,则这三个数的平方和也在
内任取三个数,则这三个数的平方和也在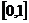 的概率为
的概率为
A.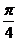 B.
B.  C.
C. 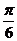 D.
D. 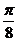
3.当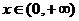 时,幂函数
时,幂函数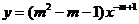 为减函数,则实数
为减函数,则实数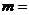
A.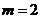 B.
B. 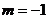 C.
C. 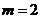 或
或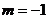 D.
D.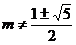
2.若非空集合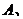
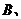
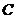 满足
满足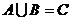 ,且
,且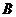 不是
不是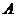 的子集,则
的子集,则
A.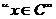 是
是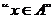 的充分不必要条件
的充分不必要条件
B.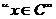 是
是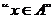 的必要不充分条件
的必要不充分条件
C.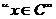 是
是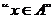 的充要条件
的充要条件
D.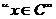 是
是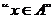 的即不充分也不必要条件
的即不充分也不必要条件
1.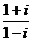 的值为
的值为
A.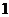 B.
B.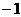 C.
C.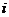 D.
D.
24.(本小题满分10分)
(1)已知实数 ,求证:
,求证: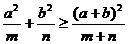 ;
;
(2) 利用(1)的结论,求函数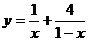 (其中
(其中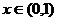 )的最小值.
)的最小值.
吉林市普通中学2009-2010学年度高中毕业班下学期期末教学质量检测
23.(本小题满分10分)
已知直线 经过点
经过点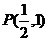 ,倾斜角
,倾斜角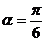 ,圆
,圆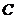 的极坐标方程为
的极坐标方程为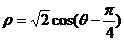
(1)写出直线 的参数方程,并把圆C的方程化为直角坐标方程;
的参数方程,并把圆C的方程化为直角坐标方程;
(2)设 与圆C相交与两点
与圆C相交与两点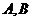 ,求点
,求点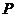 到
到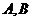 两点的距离之积.
两点的距离之积.
22.(本小题满分10分)
已知:直线AB过圆心O,交⊙O于AB, 直线AF交⊙O于AF(不与B重合),直线 与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
求证:(1)∠BAC=∠CAG;
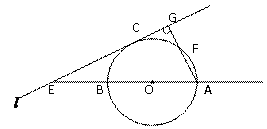
(2) 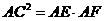 .
.
21.(本小题满分12分)
已知圆C: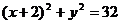 ,C为圆心,定点A
,C为圆心,定点A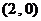 M为圆上一动点,
M为圆上一动点,
点B在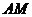 上,点N在
上,点N在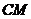 上,
上,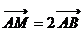 ,
, ,
,
点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)点P在(2)中的曲线E上,过点P作圆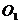 :
: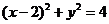
的两条切线,切点为Q、R,求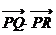 的最小值.
的最小值.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
20. (本小题满分12分)
已知函数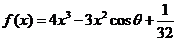 ,其中
,其中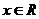 ,
,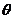 为参数,且0≤
为参数,且0≤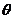 ≤
≤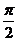 .
.
(1)当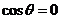 时,判断函数
时,判断函数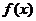 是否有极值;
是否有极值;
(2)要使函数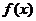 有且仅有一个零点,求
有且仅有一个零点,求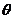 取值范围;
取值范围;
(3)若对(2)中所求的取值范围内的任意参数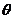 ,
,
函数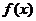 在区间
在区间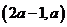 内都是增函数,求实数
内都是增函数,求实数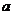 的取值范围.
的取值范围.
19. (本小题满分12分)
甲乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在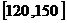 内为优秀)
内为优秀)
甲校:
|
分组 |
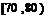 |
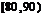 |
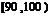 |
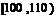 |
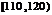 |
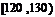 |
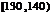 |
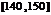 |
|
频数 |
2 |
3 |
10 |
15 |
15 |
 |
3 |
1 |
乙校:
|
分组 |
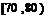 |
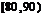 |
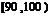 |
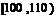 |
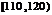 |
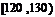 |
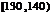 |
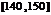 |
|
频数 |
1 |
2 |
9 |
8 |
10 |
10 |
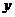 |
3 |
(1)
计算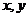 的值,并分别估计两个学校数学成绩的优秀率;
的值,并分别估计两个学校数学成绩的优秀率;
(2)
由以上统计数据填写下面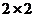 列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
|
|
甲
校 |
乙
校 |
总
计 |
|
优
秀 |
|
|
|
|
非优秀 |
|
|
|
|
总
计 |
|
|
|
附: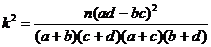
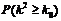 |
0.10 |
0.025 |
0.010 |
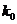 |
2.706 |
5.024 |
6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com