
13.如图是一个几何体的三视图(单位:m),则几何体的体积为 .
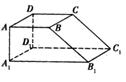 [解析]12m3 如图所示,此几何体是一个以AA1,A1D1,A1B1为棱的长方体被平面BB1C1C截去后得到的,易得其体积为长方体的体积的
[解析]12m3 如图所示,此几何体是一个以AA1,A1D1,A1B1为棱的长方体被平面BB1C1C截去后得到的,易得其体积为长方体的体积的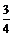 ,因为长方体的体积为2×4×2 = 16m3,故所求的体积为12m3.
,因为长方体的体积为2×4×2 = 16m3,故所求的体积为12m3.
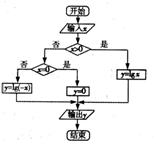
12.一个算法的程序框图如图所示,如果输出的结果在区间[–1,1]内,则输入的x的取值范围是 .
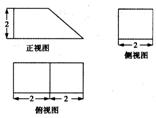 [解析]
[解析]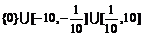 当x>0时,由y = lg x∈[–1,1]得x∈
当x>0时,由y = lg x∈[–1,1]得x∈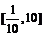 ,同理,x<0时,得x∈[–10,–
,同理,x<0时,得x∈[–10,–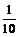 ],当x = 0时输出结果也在区间[–1,1]内.
],当x = 0时输出结果也在区间[–1,1]内.
11.已知抛物线y2 = 4x的一条过焦点的弦AB,A(x1,y1)、B(x2,
y2),AB所在直线与y轴交点坐标为(0, 2),则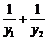 = .
= .
 [解析]
[解析]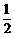 .弦AB是过焦点F(1, 0)的弦,又过点(0, 2),∴其方程为
.弦AB是过焦点F(1, 0)的弦,又过点(0, 2),∴其方程为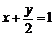 .2x + y – 2 =0与y2 = 4x联立得y2 + 2y – 4 = 0, y1 + y2 = –2, y1y2 = –4,∴
.2x + y – 2 =0与y2 = 4x联立得y2 + 2y – 4 = 0, y1 + y2 = –2, y1y2 = –4,∴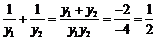 .
.
10.在图中的棋盘方格中,随机任意取两个格子,选出的两个格子不在同行的概率为 .
[解析]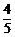 .P =
.P =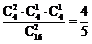 .
.
9.已知f (a)
=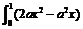 dx,则f (a)的最大值为
.
dx,则f (a)的最大值为
.
[解析]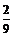
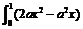 dx =
dx =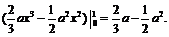
 即
即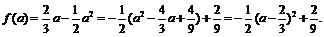 所以
所以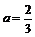 时,f (a)有最大值
时,f (a)有最大值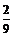 .
.
8.有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是A、B(万元),它们与投入资金x(万元)的关系近似地满足经验公式:A =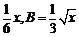 ,今有30万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为( )万元时,能获得最大利润.
,今有30万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为( )万元时,能获得最大利润.
A.15,15 B.10,20 C.29,1 D.30,0
[解析]C.设投资于甲商品x万元,总利润为y万元,则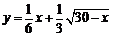 (0≤x≤30).
(0≤x≤30).
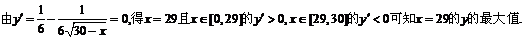
7.已知函数f (x)、g (x)(x∈R),且不等式| f (x)| + | g (x)|<a(a>0)的解集是M,不等式| f (x)| +
| g (x)|<a(a>0)的解集是N,则解集M与N的关系是( )
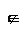 A.N M
B.M = N C.M
A.N M
B.M = N C.M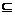 N D.M N
N D.M N
[解析]C.设x0∈M,则|f (x0)| + |g(x0)| <a (a>0).∵|f (x0) + g(x0)|≤|f (x0) |+ |g(x0)|<a,∴x0∈N,故M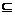 N.
N.
6.设f (x)
=x3 + log2(x +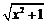 ),对任意实数a,b,都有f (a) + f (b)≥0,则( )
),对任意实数a,b,都有f (a) + f (b)≥0,则( )
A.a – b >0 B.a – b≥0 C.a + b>0 D.a + b≥0
[解析]D.显然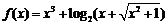 为奇函数,且单调递增.若f (a) + f (b)≥0,则f (a)≥– f (b)= f (– b),推出a≥–b,即a + b≥0.
为奇函数,且单调递增.若f (a) + f (b)≥0,则f (a)≥– f (b)= f (– b),推出a≥–b,即a + b≥0.
5.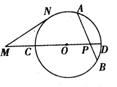 如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP = 8,PB = 6,PD = 4,MC = 6,则MN的长为( )
如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP = 8,PB = 6,PD = 4,MC = 6,则MN的长为( )
A.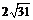 B.
B.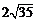 C.
C.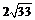 D.
D.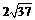
[解析]C 设圆O的半径为r,由相交弦定理得:CP·PD = AP·PB,即[r + (r – 4)]
×4 = 8×6,解得r = 8,再由切割线定理得:MN2 =
MC·MD = 6×(6 + 8×2) = 132,所以MN =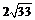 .
.
4.已知a + b + c =0, |a| = 1,|b| = 2,|c| =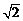 ,a·b+b·c+c·a的值为( )
,a·b+b·c+c·a的值为( )
A.7 B.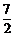 C.– 7 D.–
C.– 7 D.–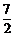
[解析]D.∵(a + b + c)2
=|a|2
+ |b|2
+ |c|2
+ 2a·b+2b·c+2a·c=1+4+2+2(a·b+b·c+c·a)=0,∴a·b+b·c+c·a =–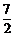 ,故选D.
,故选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com