
2.2009年7月6日,教育部、国家民委印发通知,将 教育作为专项教育纳入中小学课程,同时纳入高考及中职毕业考试。
A.爱国主义 B.集体主义 C.珍爱生命 D.民族团结
1.2009年9月15日至18日,中国共产党 全会在北京隆重召开,全会审议通过了《中共中央关于加强和改进新形势下党的建设若干重大问题的决定》。
A.十七届二中 B.十七届三中 C.十七届四中 D.十七届五中
21.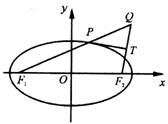 已知椭圆
已知椭圆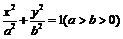 的左、右焦点分别是F1(–c,0)、F2 (c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(–c,0)、F2 (c,0),Q是椭圆外的动点,满足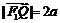 .点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足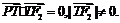
(1)设x为点P的横坐标,证明: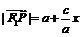 ;
;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S = b2.若存在,求∠F1MF2的正切值;若不存在,请说明现由.
[解析](1)设点P的坐标为(x,y),由P(x,y)在椭圆上,得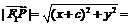
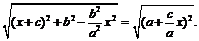
又由x≥–a,知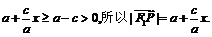 (3分)
(3分)
(2)当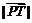 = 0时,点(a,0)和点(–a,0)在轨迹上.当
= 0时,点(a,0)和点(–a,0)在轨迹上.当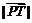 ≠0且
≠0且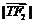 ≠0时,
≠0时,
由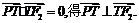 又
又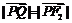 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,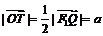 ,所以有x2 + y2 = a2. (7分)
,所以有x2 + y2 = a2. (7分)
综上所述,点T的轨迹C的方程是x2 + y2 = a2.
|
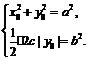
由①得|y0|≤a,由②得|y0|≤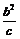 .所以,当a≥
.所以,当a≥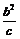 时,存在点M,使S = b2;
时,存在点M,使S = b2;
当a<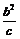 时,不存在满足条件的点M.
时,不存在满足条件的点M.
当a≥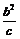 时,
时,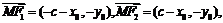
由
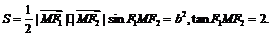 (12分)
(12分)
20.(本小题满分12分)已知函数f (x) =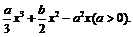 当x = x1,x = x2时有极值,且|x1| + |x2|
= 2.
当x = x1,x = x2时有极值,且|x1| + |x2|
= 2.
(Ⅰ)求a、b的关系式;
(Ⅱ)证明: ;
;
(Ⅲ)若函数h (x) = f′(x) – 2a (x – x1),证明:当x1<x<2且x1<0时|h (x)|≤4a.
[解析](Ⅰ)x1、x2是f′(x) = ax2 + bx – a2 = 0的两根
∴x1 + x2 =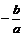 ,x1x2 = –a<0,x1、x2异号
,x1x2 = –a<0,x1、x2异号
∴|x1| + |x2| = |x1
– x2| =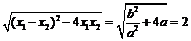
∴b2 = 4a2 – 4a3 (4分)
(Ⅱ)∵b2≥0,∴4a2 – 4a3≥0,得0<a≤1,设g (a) = 4a2 – 4a3,g′(a) = 8a – 12a2 = 4a(2 – 3a) ∴g (a)在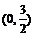 上为递增函数,
上为递增函数,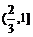 为递减函数 (6分)
为递减函数 (6分)
g (a)max = 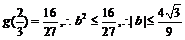 (8分)
(8分)
(Ⅲ)∵x1、x2是f′(x) = 0的两根 ∴f′(x) = a (x – x1) (x – x2)
∴h (x) = a (x – x1) (x – x2) – 2a (x – x1) = a (x – x1) (x – x2 – 2)
∴|h (x)| = |a (x
– x1) (x – x2
– 2)|≤a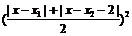 (10分)
(10分)
又∵x>x1,∴|x – x1| = x – x1.又∵x1<0,x1x2 = –a<0,∴x2>0
x2 + 2>2且x<2 ∴|x – x2 – 2| = |x2 + 2 – x| = x2 + 2 – x,|x2 – x1 | = x2 – x1 = 2
∴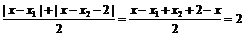
∴|h (x)|≤4a. (12分)
19.(本小题满分13分)已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超越原有员工的5%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数x不超过原有员工的1%时,留岗员工每人每年可为企业多凶暴利润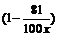 万元;当待岗员工人数x超越原有员工的1%时,留岗员工每人每年可为企业多创利润0.9595万元.为使企业年利润最大,应安排多少员工待岗?
万元;当待岗员工人数x超越原有员工的1%时,留岗员工每人每年可为企业多创利润0.9595万元.为使企业年利润最大,应安排多少员工待岗?
[解析]设重组后,该企业年利润为y万元.∵2000×1% = 20,
∴当0<x≤20且x∈N时,y = (2000 – x) (3.5 + 1 – 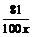 ) – 0.5x = –5
) – 0.5x = –5 + 9000.81.
+ 9000.81.
∵x≤2000×5%,∴x≤100,∴当20<x≤100且x∈N时,
y = (2000 – x) (3.5 + 0.9595) – 0.5x = –4.9595 x + 8919.
∴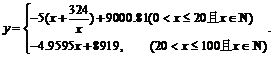
当0<x≤20时,有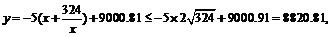
当且仅当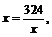 即x = 18时取等号,此时y取得最大值8820.81.
即x = 18时取等号,此时y取得最大值8820.81.
当20<x≤100时,函数y = –4.9595x + 8919为函数,
所以y<–4.9595×20 + 8919 = 8819.81.
综上所述x = 18时,y有最大值8820.81万元.即要使企业年利润最大,应安排18名员待岗.
18.(本小题满分12分)某校高一(1)班的课外生物研究小组通过互联网上获知,某种珍稀植物种子在一定条件下发芽成功率为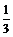 ;小组依据网上介绍的方法分小组进行验证性实验(每次实验相互独立).
;小组依据网上介绍的方法分小组进行验证性实验(每次实验相互独立).
(Ⅰ)第一小组共做了5次种子发芽的实验(每次均种下一粒种子),求5次实验至少有3次成功的概率;
(Ⅱ)第二小组在老师的带领下做了若干次实验(每次均种下一粒种子),如果在一次实验中,种子发芽成功则停止实验;否则将继续进行下去,直到种子发芽成功为止,而该小组能供实验的种子只有n颗(n≥5,n∈N*).求第二小组所做的实验次数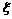 的概率分布列和数学期望.
的概率分布列和数学期望.
[解析](Ⅰ)由题设可知这5次实验即为5次独立重复实验,则至少3次成功的概率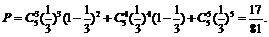 (4分)
(4分)
(Ⅱ)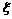 的可能取值为1,2,3,…,n,其分布列为
的可能取值为1,2,3,…,n,其分布列为
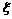 |
1 |
2 |
3 |
4 |
… |
n – 1 |
n |
|
P |
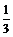 |
 |
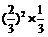 |
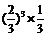 |
… |
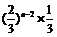 |
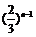 |
(7分)
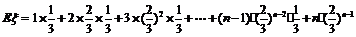
= 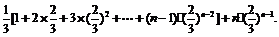 (8分)
(8分)
令Sn = 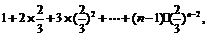
则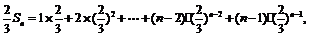
两式相减得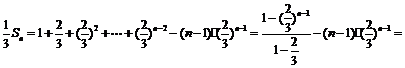
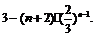 所以Sn = 9 – 3(n + 2)·
所以Sn = 9 – 3(n + 2)·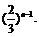
故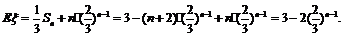 (12分)
(12分)
17.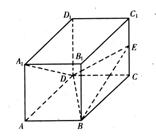 (本小题满分12分)如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD = BD = a,E是CC1的中点,A1D⊥BE.
(本小题满分12分)如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD = BD = a,E是CC1的中点,A1D⊥BE.
(Ⅰ)求证:A1D⊥平面BDE;
(Ⅱ)求二面角B-DE-C的大小.
[解析](Ⅰ)∵直平行六面体ABCD-A1B1C1D1中,A1A⊥平面ABCD,又∵AD⊥BD,∴A1D⊥BD,又A1D⊥BE,∴A1D⊥平面BDE. (4分)
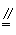
 (Ⅱ)连B1C,∵A1B1 CD,∴B1C A1D.∵A1D⊥BE,∴B1C⊥BE,
(Ⅱ)连B1C,∵A1B1 CD,∴B1C A1D.∵A1D⊥BE,∴B1C⊥BE,
 ∴∠BB1C = ∠CBE.∴Rt△BB1C∽Rt△CBE,
∴∠BB1C = ∠CBE.∴Rt△BB1C∽Rt△CBE,
∴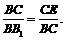 又∵CE =
又∵CE =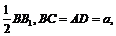
∴ ,
,
取CD取中点M,连BM,∵CD = .
.
过M作MN⊥DE于N,连BN.∵BM⊥平面CD1,
∴BN⊥DE,∴∠BNM就是二面角B-DE-C的平面角, (8分)
∵sin∠MDN =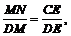 DE =
DE =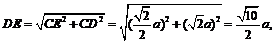
∴MN =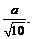
在Rt△BNM中,tan∠BNM =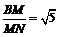 .
.
即二面角B-DE-C的大小等于arctan . (12分)
. (12分)
16.(本小题满分10分)在锐角△ABC中,a、b、c分别是内角A、B、C的对边,S是该三角形的面积,且4sinB sin2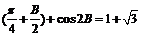 .
.
(Ⅰ)求角B的度数;
(Ⅱ)已知a = 4,S = 5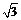 ,求b的值.
,求b的值.
[解析](Ⅰ)因为4sinB sin2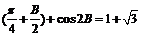 ,
,
所以4sinB·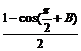 + (1 – 2sin2B)
= 1 +
+ (1 – 2sin2B)
= 1 +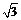 , (3分)
, (3分)
即2sinB + 2sin2B + 1 – 2sin2B
= 1 +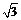 ,所以sinB =
,所以sinB =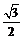 .
.
因为0<B<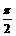 ,所以B =
,所以B =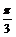 . (6分)
. (6分)
(Ⅱ)因为a = 4,S =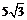 ,所以由S =
,所以由S = ac sinB,得5
ac sinB,得5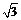 =
=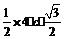 ,
,
所以c = 5. (8分)
又B =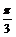 ,所以b2 = a2 + c2 –
2ac cosB = 42 + 52 – 2×4×5×
,所以b2 = a2 + c2 –
2ac cosB = 42 + 52 – 2×4×5× = 21.
= 21.
所以b =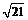 . (10分)
. (10分)
15.在等差数列{an}中,a1为首项,Sn是其前n项的和,将Sn =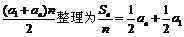 后可知:点
后可知:点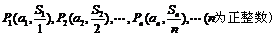 都在直线
都在直线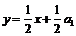 上,类似地,若{an}是首项为a1,公比为q (q≠1)的等比数列,则点P1(a1,S1),P2 (a2,S2),…,Pn (an,Sn) (n为正整数)在直线
上.
上,类似地,若{an}是首项为a1,公比为q (q≠1)的等比数列,则点P1(a1,S1),P2 (a2,S2),…,Pn (an,Sn) (n为正整数)在直线
上.
[解析]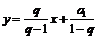 因为
因为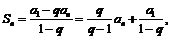
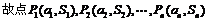 …在直线
…在直线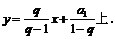
14.已知点M(a, b)在由不等式组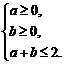 确定的平面区域内,则点N(a+b, a–b)构成的平面区域的面积是
.
确定的平面区域内,则点N(a+b, a–b)构成的平面区域的面积是
.
[解析]4.由题意得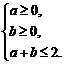 令x = a+b,y = a
– b,则
令x = a+b,y = a
– b,则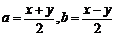 ,
,
即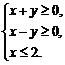 点N(x,y)所在的平面区域是△ABO的内部及边界,其中A(2,2),B(2, –2),
点N(x,y)所在的平面区域是△ABO的内部及边界,其中A(2,2),B(2, –2),
∠AOB = 90°,则S△ABO = 4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com