
20.某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为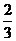 .
.
(Ⅰ)求比赛三局甲获胜的概率;
(Ⅱ)求甲获胜的概率;
(Ⅲ)设甲比赛的次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
19.道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车. 某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:
(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;
18.下表为某体育训练队跳高成绩的分布,共有队员40人,成绩分为1~5五个档次,例如表中所示跳高成绩为4分,跳远成绩为2分的队员为5人。将全部队员的姓名卡混合在一起,任取一张,该卡片队员的跳高成绩为x,跳远成绩为y,设x,y为随即变量(注:没有相同姓名的队员)
(Ⅰ)求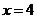 的概率及
的概率及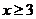 且
且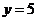 的概率;
的概率;
(Ⅱ)求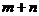 的值;若y的数学期望为
的值;若y的数学期望为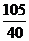 ,求m,n的值.
,求m,n的值.
|
y x |
跳
远 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
跳 高 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
2 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
4 |
3 |
|
|
2 |
1 |
m |
6 |
0 |
n |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
17.极坐标方程为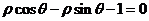 的直线L与
的直线L与 轴的交点为
轴的交点为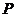 ,与曲线
,与曲线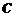
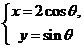 (
(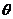 为参数)交于
为参数)交于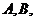
(Ⅰ)写出曲线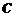 和直线L的直角坐标方程;(Ⅱ)求
和直线L的直角坐标方程;(Ⅱ)求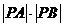 .
.
16.将1,2,3填入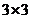 的方格中,要求每行、每列都没有重复
的方格中,要求每行、每列都没有重复
数字,下面是一种填法,则不同的填写方法共有 种

15、在极坐标系中,已知两点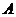 、
、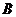 的极坐标分别为
的极坐标分别为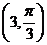 ,
,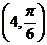 ,则△
,则△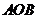 (其中
(其中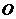 为极点)的面积为 .
为极点)的面积为 .
14.在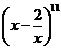 的展开式中,
的展开式中,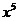 的系数为__ ___.
的系数为__ ___.
13.在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,在第一次抽到理科题的条件下,第2次也抽到理科题的概率为______ __
12.已知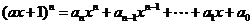
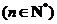 ,点列
,点列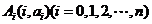 部分图象如图所示,则实数
部分图象如图所示,则实数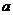 的值为( )
的值为( )
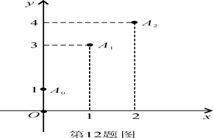
A.1 B.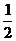 C.
C. D.
D.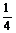
11.下列四个命题
①相关关系和函数关系都属于完全确定性的依存关系。
②残差平方和越小的模型,拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
④随机误差e是衡量预报精确度的一个量,它满足E(e)=0
其中正确命题的序号是( )
A.①③ B.②④ C.①④ D.②③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com