
18.(本小题满分12分)
设角 是
是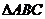 的三个内角,已知向量
的三个内角,已知向量 ,
,
 ,且
,且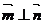 .
.
 (Ⅰ)求角
(Ⅰ)求角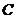 的大小; (Ⅱ)若向量
的大小; (Ⅱ)若向量 ,试求
,试求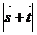 的取值范围.
的取值范围.
17.(本小题满分12分)
把一个棋子放在△ABC的顶点A,棋子每次跳动只能沿△ABC的一条边从一个顶点跳到另一个顶点,并规定:抛一枚硬币,若出现正面朝上,则棋子按逆时针方向从棋子所在的顶点跳到△ABC的另一个顶点;若出现反面朝上,则棋子按顺时针方向从棋子所在的顶点跳到△ABC的另一个顶点。现在抛3次硬币,棋子按上面的规则跳动3次
 (Ⅰ)列出棋子从起始位置A开始3次跳动的所有路径(用△ABC顶点的字母表示);
(Ⅰ)列出棋子从起始位置A开始3次跳动的所有路径(用△ABC顶点的字母表示);
(Ⅱ)求3次跳动后,棋子停在A点的概率.
16.定义函数 ,若存在常数C,对任意的
,若存在常数C,对任意的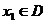 ,存在唯一的
,存在唯一的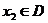 ,使得
,使得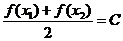 ,则称函数
,则称函数 在D上的均值为C。已知
在D上的均值为C。已知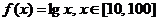 ,则函数
,则函数 上的均值为
上的均值为
15. 以下有四种说法:
(1)若 ,则
,则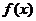 在
在 处取得极值;
处取得极值;
(2)由变量x和y的数据得到其回归直线方程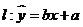 ,则
,则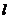 一定经过点
一定经过点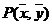 ;
;
(3)若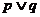 为真,
为真, 为假,则
为假,则 与
与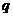 必为一真一假;
必为一真一假;
(4)函数 最小正周期为π,其图象的一条对称轴为
最小正周期为π,其图象的一条对称轴为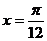 .
.
以上四种说法,其中正确说法的序号为 .
14.若平面区域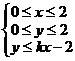 是一个梯形,则实数
是一个梯形,则实数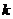 的取值范围是________
的取值范围是________
13.为了解某校教师使用多媒体进行教学的情况,采用简单随
 机抽样的方法,从该校200名授课教师中抽
机抽样的方法,从该校200名授课教师中抽 取20名教师,
取20名教师,
调查了他们上学期使用多媒体进行教学的次数,结果用茎
叶图表示如下:据此可估计该校上学期200名教师中,使用
多媒体进行教学次数在 内的人
内的人 数为
数为
12. 如图,在平面斜坐标中
如图,在平面斜坐标中 ,斜坐标定义为
,斜坐标定义为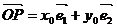 (其中
(其中 分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为
分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为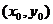 .若
.若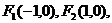 且动点
且动点 满足
满足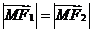 ,则点M在斜坐标系中的轨迹方程(
)
,则点M在斜坐标系中的轨迹方程(
)
A.  B.
B.
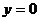
C.  D.
D.

11.已知直线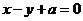 与圆
与圆 交于不同两点
交于不同两点 、
、 ,
, 为坐标原点,则“
为坐标原点,则“ ”是“向量
”是“向量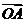 、
、 满足
满足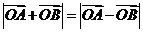 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
10.已知 是双曲线
是双曲线 上不同的三点,且
上不同的三点,且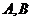 连线经过坐标原点,若直线
连线经过坐标原点,若直线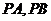 的斜率乘积
的斜率乘积 ,则该双曲线的离心率为 ( )
,则该双曲线的离心率为 ( )
A.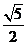 B.
B. C.
C. D.
D.
9.设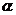 、
、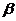 、
、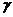 是三个不同的平面,a、b是两条不同的直线,下列四个命题中正确的是( )
是三个不同的平面,a、b是两条不同的直线,下列四个命题中正确的是( )
A.若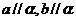 ,则
,则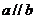 B.若
B.若 ,则
,则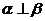 K^S*5U.C
K^S*5U.C
C.若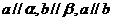 ,则
,则 D.若
D.若 在平面
在平面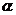 内的射影互相垂直,则
内的射影互相垂直,则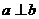
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com