
2. 给定空间中的直线l及平面a,条件“直线l与平面a内无数条直线都垂直”是“直线l与平面a垂直”的( )条件
A.充要 B.充分非必要 C.必要非充分 D.既非充分又非必要
1.用与球心距离为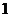 的平面去截球,所得的截面面积为
的平面去截球,所得的截面面积为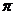 ,则球的体积为( )
,则球的体积为( )
A. 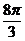 B.
B.
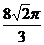 C.
C.
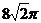 D.
D.
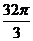
4.空间向量与空间角和距离的综合
用空间向量解决立体几何问题的基本步骤:(1)用空间向量表示问题中涉及的点、直线、平面,建立立体图形与空间向量的联系,从而把立体几何问题转化为向量问题(几何问题向量化);(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹我有等问题(进行向量运算);(3)把向量的运算结果“翻译”成相应的几何意义(回归几何问题).
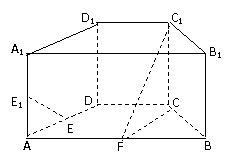 例6. 如图,在直四棱柱ABCD-A
例6. 如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA =2, E、E
=2, E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点.
、AB的中点.
(1) 证明:直线EE //平面FCC
//平面FCC ;
;
(2) 求二面角B-FC -C的余弦值.w.w.w.k.s.5.u.c.o.m
-C的余弦值.w.w.w.k.s.5.u.c.o.m
解析:解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
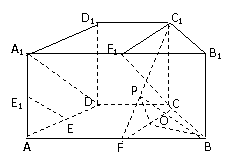 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为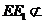 平面FCC
平面FCC ,
,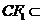 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,
取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A B
B C
C D
D 中,CC1⊥平面ABCD,
中,CC1⊥平面ABCD,
所以CC1⊥BO,所以OB⊥平面CC1F,
过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角,
-C的一个平面角,
在△BCF为正三角形中,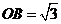 ,
,
在Rt△CC1F中, △OPF∽△CC1F,∵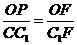 ∴
∴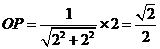 , w.w.w.k.s.5.u.c.o.m
, w.w.w.k.s.5.u.c.o.m
在Rt△OPF中,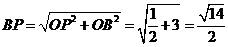 ,
,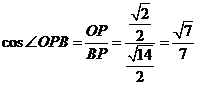 ,
,
所以二面角B-FC -C的余弦值为
-C的余弦值为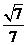 .
.
 解法二:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
解法二:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0,0,0),A(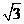 ,-1,0),F(
,-1,0),F(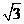 ,1,0),C(0,2,0),C1(0,2,2),E(
,1,0),C(0,2,0),C1(0,2,2),E(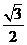 ,
,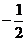 ,0),E1(
,0),E1(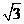 ,-1,1),
,-1,1),
所以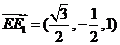 ,
,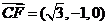 ,
,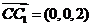
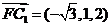
设平面CC1F的法向量为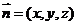 则
则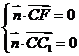 所以
所以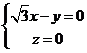
取 ,则
,则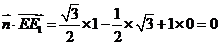 ,所以
,所以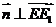 ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
.
(2)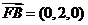 ,设平面BFC1的法向量为
,设平面BFC1的法向量为 ,则
,则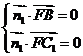 所以
所以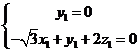 ,取
,取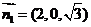 ,则
,则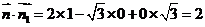 ,
,
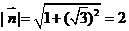 ,
,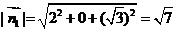 ,所以
,所以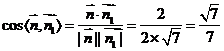 ,
,
由图可知二面角B-FC -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC -C的余弦值为
-C的余弦值为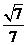 .
.
点评:本题主要考查直棱柱的概念、线面位置关系的判定和二面角的计算.考查空间想象能力和推理运算能力,以及应用向量知识解答问题的能力,向量法求二面角是一种独特的方法,因为它不但是传统方法的有力补充,而且还可以另辟溪径,解决传统方法难以解决的求二面角问题.向量法求二面角通常有以下三种转化方式:①先作、证二面角的平面角 ,再求得二面角的大小为
,再求得二面角的大小为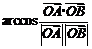 ;②先求二面角两个半平面的法向量
;②先求二面角两个半平面的法向量 (注意法向量的方向要分布在二面角的内外),再求得二面角的大小为
(注意法向量的方向要分布在二面角的内外),再求得二面角的大小为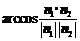 或其补角;③先分别在二面角两个半平面内作棱的垂线(垂足不重合),又可转化为求两条异面直线的夹角.
或其补角;③先分别在二面角两个半平面内作棱的垂线(垂足不重合),又可转化为求两条异面直线的夹角.
[思想方法]
[例1]在半径为13的球面上有A , B, C 三点,AB=6,BC=8,CA=10,则球心到平面ABC的距离为 .
答案:12解析:由 的三边大小易知此三角形是直角三角形,所以过
的三边大小易知此三角形是直角三角形,所以过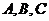 三点小圆的直径即为10,也即半径是5,设球心到小圆的距离是
三点小圆的直径即为10,也即半径是5,设球心到小圆的距离是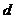 ,则由
,则由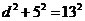 ,可得
,可得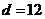 .
.
[分析]该题体现了方程函数思想的考查,构造方程求解立体几何中的几何量是考题中经常性的问题,其解法一般要根据题意构造方程来求解.
[例2]已知二面角α-l-β为 ,动点P、Q分别在面α、β内,P到β的距离为
,动点P、Q分别在面α、β内,P到β的距离为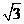 ,Q到α的距离为
,Q到α的距离为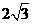 ,则P、Q两点之间距离的最小值为( )
,则P、Q两点之间距离的最小值为( )
A.1 B.2
C.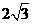 D.4
D.4
解析:如图分别作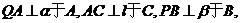
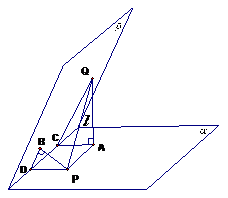
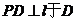 ,连
,连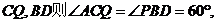
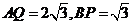 ,
,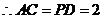
又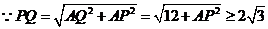
当且仅当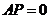 ,即
,即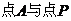 重合时取最小值.
重合时取最小值.
故答案选C.
[分析]该题考查了函数思想和数形结合思想,立体几何中的最值问题一般要用函数法或均值不等式法,该题通过构造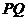 关于
关于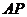 的函数,借助图象看出当
的函数,借助图象看出当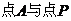 重合时取最小值.
重合时取最小值.
[例3]已知正四棱柱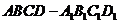 中,
中,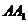 =
=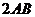 ,
,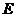 为
为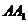 重点,则异面直线
重点,则异面直线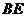 与
与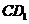 所形成角的余弦值为
所形成角的余弦值为
A.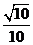 B.
B. 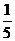 C.
C.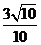 D.
D.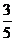
解析:本题考查异面直线夹角求法,利用平移,CD'∥BA' ,因此求△EBA'中∠A'BE即可,易知EB=
,因此求△EBA'中∠A'BE即可,易知EB=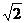 ,A'E=1,A'B=
,A'E=1,A'B= ,故由余弦定理求cos∠A'BE=
,故由余弦定理求cos∠A'BE=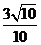 .
.
答案:C
[分析]该题体现了转化与化归思想的考查,对与异面直线的夹角的求解,一种方法是通过这种平移的方法将所求的夹角转化为三角形中的内角,通过解三角形即可.另一种是利用空间向量这一工具来求解.
[专题演练]
3.几何体与线、面位置关系的综合
以空间几何体为载体考查直线与平面平行或垂直、平面与平面平行或垂直的判定与性质定理,能用判定定理和性质定理证明线线平行或垂直、线面平行或垂直、面面平行或垂直,多以选择题和解答题形式出现,解答题中多以证明线线垂直、线面垂直、面面垂直为主,属中档题.
例5. 正方体ABCD-A1B1C1D1中O为正方形ABCD的中心,M为BB1的中点,
求证: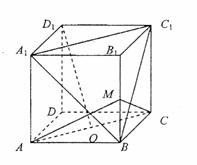 (1)D1O//平面A1BC1;
(1)D1O//平面A1BC1;
(2)D1O⊥平面MAC.
证明:
(1)连结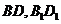 分别交
分别交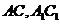 于
于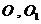
在正方体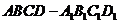 中,对角面
中,对角面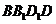 为矩形
为矩形
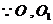 分别是
分别是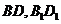 的中点
的中点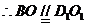
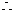 四边形
四边形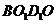 为平行四边形
为平行四边形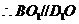
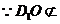 平面
平面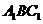 ,
,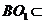 平面
平面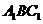
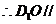 平面
平面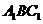
(2)连结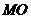 ,设正方体
,设正方体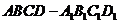 的棱长为
的棱长为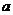 ,
,
在正方体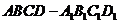 中,对角面
中,对角面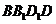 为矩形且
为矩形且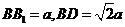
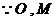 分别是
分别是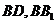 的中点
的中点
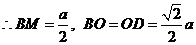
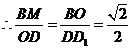
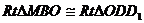
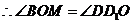
 在
在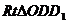 中,
中,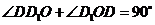
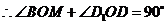 ,即
,即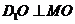
在正方体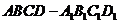 中
中
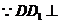 平面
平面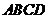
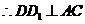
又 ,
,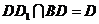
 平面
平面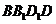
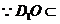 平面
平面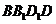
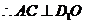
又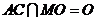
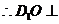 平面
平面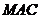
点评:证明线面垂直,关键是在平面内找到两条相交直线与已知直线垂直,由线线垂直推出线面垂直,证明线线垂直有时要用勾股定理的逆定理.
2.三视图与几何体的面积、体积的综合
空间几何体的结构与视图主要培养观察能力、归纳能力和空间想象能力,识别三视图所表示的空间几何体,柱、锥、台、球体及其简单组合体的结构特征与新增内容三视图的综合会重点考查,新课标地区的高考题来看,三视图是出题的热点,题型多以选择题、填空题为主,属中等偏易题.随着新课标的推广和深入,难度逐渐有所增加.
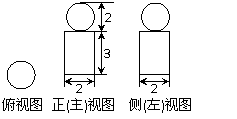
例3. 右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.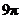 B.
B.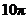 C.
C.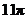 D.
D.

答案:D
解析:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的简单几何体,其表面及为: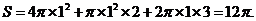 ,故选D.
,故选D.
点评:本小题主要考查三视图与几何体的表面积.既要能识别简单几何体的结构特征,又要掌握基本几何体的表面积的计算方法.
例4.若某几何体的三视图(单位: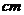 )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是
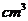 .
.
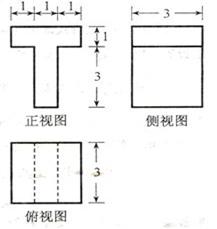 答案:18
答案:18
解析:该几何体是由两个长方体组成,下面体积为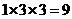 ,上面的长方体体积为
,上面的长方体体积为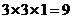 ,因此其几何体的体积为18.
,因此其几何体的体积为18.
点评:此题主要是考查了几何体的三视图,通过三视图的考查充分体现了几何体直观的考查要求,与表面积和体积结合的考查方法.
1.充分、必要条件与点线面位置关系的综合
高考对简单逻辑用语中的充分、必要条件的考查,主要通过与其它部分的综合问题出现,而与立体几何相综合的问题最为普遍,通过这种形式主要考查对充分、必要条件的理解和立体几何部分的几何体、点线面的位置关系等严密性问题.
例1.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“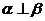 ”是“
”是“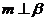 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
答案:B
解析:由平面与平面垂直的判定定理知,如果m为平面α内的一条直线,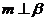 ,则
,则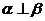 ;反过来则不一定.所以“
;反过来则不一定.所以“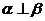 ”是“
”是“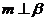 ”的必要不充分条件.
”的必要不充分条件.
例2.设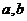 是两条直线,
是两条直线,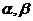 是两个平面,则
是两个平面,则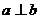 的一个充分条件是( )
的一个充分条件是( )
(A) (B)
(B)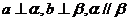
(C) (D)
(D)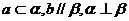
答案:C
解析:由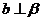 ,
,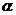 ∥
∥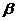 得
得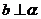 ,又
,又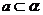 ,因此可知
,因此可知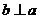 ,故
,故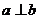 的一个充分条件是C,选C.
的一个充分条件是C,选C.
点评:此类题目主要考查了立体几何中垂直关系的判定和充分必要条件的概念.解决此类问题的关键是弄清楚点线面之间的位置关系的判定.此类小题是很容易出错的题目,解答时要特别注意.
2. 立体几何考查的重点有:空间几何体的结构特征、空间几何体的侧面积、表面积和体积、直线与平面、平面与平面之间的位置关系,三视图是新教材的内容,已经成为了必考的重点知识点.等体积转化法、割补思想是该部分考查的主要思想方法.
[知识交汇]
1. 立体几何内容既承担着对逻辑思维能力的考查,又承担着对空间想象能力的考查,常以选择题、填空题的形式全面考查线线、线面、面面等空间位置关系,难度适中,纵观历年的高考题一定有一个立体几何的解答题,考查平行、垂直的证明及面积、体积的计算等,难度中等,理科还可以以空间向量为工具证明位置关系或求空间中的角和距离等.高考的另一个新趋势是以立体几何为载体,考查函数、解析几何等的知识交汇点的综合题.
6. 下图表示各物质之间的转化关系。已知:
Ⅰ.A是无色液体,L是不溶于稀硝酸的白色沉淀,E、F、H、J、X、Y、Z是气体;
Ⅱ.G、X、Y、Z是单质,其它是化合物,其中Y呈黄绿色、H呈红棕色,E和F都极易溶解于水,二者相遇会有白烟生成;
Ⅲ.B和C都是由一种金属与一种非金属元素组成的化合物,其中非金属元素相同且质量分数都是28%,组成B的金属元素原子核外的K层和M层电子数相同。
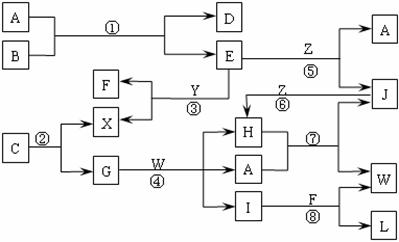
请按要求填空:
⑴写出下列物质的电子式:A________________,X________________;
⑵工业上制取硝酸的反应有(填写反应代号):_____________________;
⑶写出下列物质的化学式:B___________,C___________;
⑷反应④的化学方程式为:_____________________________________________。
⑸保持容器的温度和体积不变,在反应③刚好完全发生时,反应前后容器的压强之比为__________。
5. A、B、C、D分别代表硝酸银、偏铝酸钠、稀盐酸、浓氨水四种无色溶液中的一种。甲、乙两同学分别用两两混合的方法进行了如下图所示的实验,现象有的相同,有的不同,不同部分已标出。
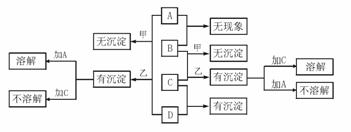
⑴试写出A、B、C、D所代表物质的化学式:
A:____________、B:____________、C:____________、D:____________。
⑵写出B和C按物质的量之比为1:3时反应的化学方程式_____________________。
⑶写出A和D按物质的量之比为3:1时反应的离子方程式_____________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com