
本部分共35题,每题4分,共140分。在每题给出的四个选项中,只有一项是最符合题目要求的。
19.(12分)等差数列 的前
的前 项和为
项和为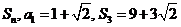 .
.
(1)求数列 的通项
的通项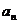 与前
与前 项和
项和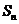 ;
;
(2)设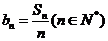 ,数列
,数列 中是否存在不同的三项能成为等比数列. 若存在则求出这三
中是否存在不同的三项能成为等比数列. 若存在则求出这三
项,若不存在请证明.
命题人:周 强
审题人:王 明
重庆一中高2010级高三下期4月月考
16.(13分)已知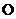 为坐标原点,
为坐标原点,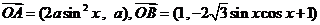 ,
,
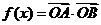
 ,其中
,其中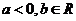 .
.
(1)求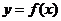 的单调递增区间;
的单调递增区间;
(2)若 的定义域为
的定义域为 ,值域为[2,5],求
,值域为[2,5],求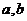 的值.
的值.
15.设直线 与球
与球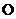 有且仅有一个公共点P.从直线
有且仅有一个公共点P.从直线 出发的两个半平面截球
出发的两个半平面截球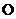 的两个截面圆
的两个截面圆
和圆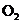 的半径分别为3和2,若这两个半平面
的半径分别为3和2,若这两个半平面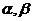 所成的二面角为120°.则球
所成的二面角为120°.则球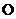 的半径
的半径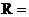
_______________.
14.已知平面区域D由以A(1,3), B(5,2), C(3,1)为顶点的三角形内部和边界组成,若在区域D
上有无穷多个点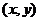 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则 = .
= .
13.篮球明星易建联在三分线外投篮6次,若每次投篮进球的概率均为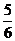 ,则他这6次投篮进球的
,则他这6次投篮进球的
个数 的方差
的方差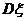 =
__.
=
__.
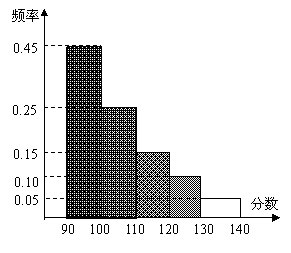
12.某校高三数学考试中,对90分以上(含90分)
的成绩进行统计,频率分布如图所示,130-140
分数段的人数为40人,则90-110分数段的人
数为 .
11. .
.
10.已知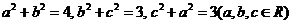 ,则
,则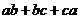 的最小值为( )
的最小值为( )
 A.
A. B.
B.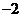 C.
C.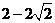 D.
D.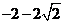
9.下列4个命题:
①存在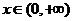 ,满足
,满足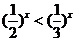 ; ②存在
; ②存在 ,满足
,满足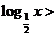
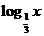 ;
;
③任意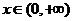 ,都有
,都有 ; ④任意
; ④任意 ,都有
,都有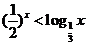 ;
;
其中真命题是( )
A.①③ B. ①④ C.②③ D.②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com