23．(本小题满分10分)

　　 以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1，-5)，点M的极坐标为若直线l过点P，且倾斜角为，圆C以M为圆心、4为半径。

　 (I)求直线l的参数方程和圆C的极坐标方程；

　 (II)试判定直线l和圆C的位置关系。

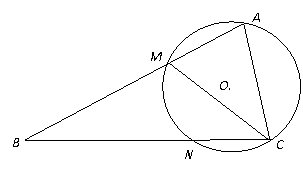
22．选修4－1：几何证明选讲

　 　　 在中,是的平分线,的外接圆交于点,且 ．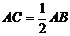　

　 　　 求证: ．

　　　　 选修4-4：坐标系与参数方程

21．(本小题满分12分)

　 设椭圆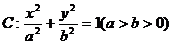的离心率，右焦点到直线的距离

　 O为坐标原点。

　 (I)求椭圆C的方程；

　 (II)过点O作两条互相垂直的射线，与椭圆C分别交于A，B两点，证明: 点O到直线AB的距离为定值，并求弦AB长度的最小值。

_{四、选考题(本题满分10分。请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分)}

20．(本小题满分12分)

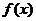　　 已知函数是的导函数。

　 (I)当a=2时，对于任意的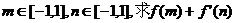的最小值；

　 (II)若存在，使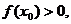求a的取值范围。

19．(本小题满分12分)

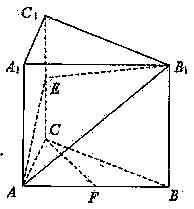
　　　　 如图，已知直三棱柱ABC-A₁B₁C₁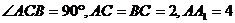，。E、F分别是棱CC₁、AB中点。

　 (1)求证：；

　 (2)求四棱锥A-ECBB₁的体积；

　 (3)判断直线CF和平面AEB₁的位置关系，并加以证明。

18．(本小题满分12分)

　　 设数列{a_n}的前n项和为S_n，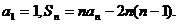

　 (I)求证: 数列{a_n}是等差数列;

　 (II)设数列的前n项和为T_n，求T_n．

17．(本小题满分共12分)

　　　　 　　 为了让学生更多的了解“数学史”知识，某中学高二年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有名学生参加了这次竞赛．为解本 次竞赛的成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为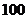分)进行统计．请你根据频率分布表，解答下列问题：

　 (Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案)；

序号()	分组(分数)	组中值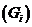	频数(人数)	频率
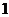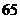			①
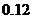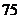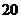				②
			③
			④	⑤
合计

　 (Ⅱ)为鼓励更多的学生了解“数学史”知识，成绩不低于分的同学能获奖，请估计在参加的　　 名学生中大概有多少同学获奖？

　 (Ⅲ)在上述统计数据的分析中有一项计算 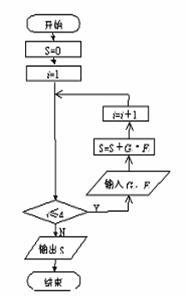　 见算法流程图，求输出的值．

16．锐角三角形ABC中，若A=2B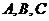，所对的边分别为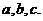则下列四个结论:

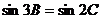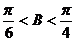　　 ①　　 ② ③　　　　　 ④

　　 其中正确的是________．

15．若过点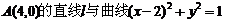有公共点，则直线l的斜率的取值范围为________．

14．若曲线f(x)=x·sinx+1在x=处的切线与直线ax+2y+1=0互相垂直，则实数a等于

_______．