
23.选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是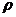 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为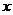 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线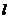 的参数方程是
的参数方程是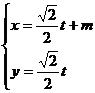 (
(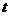 是参数)。
是参数)。
⑴将曲线C的直角坐标方程和直线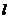 的参数方程转化为普通方程。
的参数方程转化为普通方程。
⑵若直线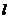 与曲线C相交于A、B两点,且|AB|=
与曲线C相交于A、B两点,且|AB|=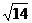 ,试求实数
,试求实数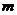 的值。
的值。
22.选修4-1:几何证明选讲
⊙O如图: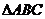 是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
⑴求证: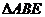
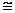
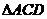 ;
;
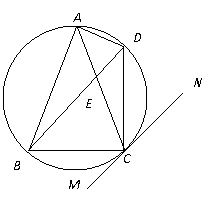 ⑵若AB=6,BC=4,求AE。
⑵若AB=6,BC=4,求AE。
21.(本小题12分)已知函数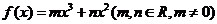 ,函数
,函数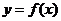 的图象在点
的图象在点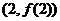 处切线与x轴平行,
处切线与x轴平行,
(1)用关于m的代数式表示n;
(2)求函数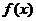 的单调递增区间;
的单调递增区间;
(3)若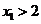 ,记函数
,记函数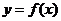 的图象在点
的图象在点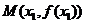 处的切线
处的切线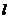 与
与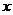 轴的交点为
轴的交点为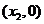 ,证明:
,证明: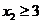 .
.
请考生在第22,23,24三题中任选一题做答,如果多做,则按所做的第一题计分。
(本小题满分10分)
20.(本小题满分12分)
已知向量\S\UP6(→=(2,0),O是坐标原点,动点 M 满足:| \S\UP6(→+ \S\UP6(→|+| \S\UP6(→-\S\UP6(→| = 6。
(1)求点 M 的轨迹 C 的方程;
(2)是否存在直线 l 过 D(0,2)与轨迹 C 交于 P、Q 两点,且以 PQ 为直径的圆过原点,若存在,求出直线 l 的方程;若不存在,说明理由.
19.(本小题满分12分)
如图,在底面为直角梯形的四棱锥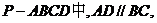
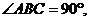

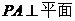
 ,
,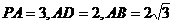 ,
,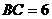
(Ⅰ)求证: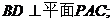
(Ⅱ)求二面角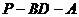 的大小.
的大小.
18.(本小题满分12分)
“ 五·一”黄金周某旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条旅游线路.
(Ⅰ)求3个旅游团选择3条不同的线路的概率;
(Ⅱ)求恰有2条线路被选择的概率;
(Ⅲ)求选择甲线路的旅游团个数的期望.
17.(本小题满分12分)
已知向量m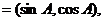 n
n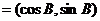 , m .n
, m .n 分别为△ABC的三边a,b,c所对的角.
分别为△ABC的三边a,b,c所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA, sinC, sinB成等比数列, 且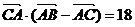 , 求c的值.
, 求c的值.
16.定义一种运算“*”,它对正整数n满足以下运算:
(1)2*1001=1;
(2)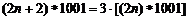 ,则2008*1001的值是 .
,则2008*1001的值是 .
15.已知正四棱柱ABCD-A1B1C1D1的底面ABCD边长为1,高AA1=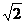 ,它的八个顶点都在同一球面上,那么球的半径是 .
,它的八个顶点都在同一球面上,那么球的半径是 .
14.某校准备召开高中毕业生代表会,把6个代表名额分配给高三年级的3个班,每班至少一个名额,不同的分配方案共有 种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com