
2.下列命题错误的是()
A.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x 1,则x2-3x+2
1,则x2-3x+2 0”
0”
B.若命题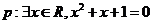 ,则
,则
C.若p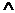 q为假命题,则p,q均为假命题
q为假命题,则p,q均为假命题
 D.“X>2”是“x2-3x+2>0”的充分不必要条件
D.“X>2”是“x2-3x+2>0”的充分不必要条件
1.若 是纯虚数,则
是纯虚数,则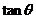 的值为()
的值为()
A.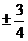 B.
B.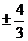 C.
C.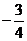 D.
D.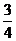
22.已知函数f(X)=ax3+bx2-3x在x=±1处取得极值。
(1)求函数f(x)的解析式;
(2)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|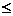 4;
4;
(3)若过点A(1,m) 可作曲线y=f(x)的三条切线,求实数m的取值范围。
可作曲线y=f(x)的三条切线,求实数m的取值范围。
文科数学试题(二)第4页(共4页)



21.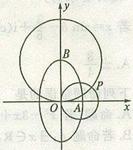 如图,设椭圆
如图,设椭圆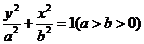 的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P。
的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P。
(1)若点P在直线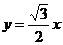 上,求椭圆的离心率;
上,求椭圆的离心率;
(2)在(1)的条件下,设M是椭圆上一动点,且点 N(0,1)到椭圆上的点的最近距离为3,求椭圆的方程。
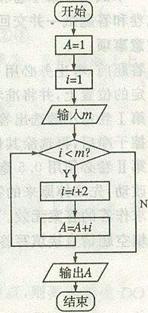
20.请看右边的程序框图:
若依次输入m=0,1,2,3,4,……,(m N),则由右边程序框图输出的数值A组成一个数列{an}。
N),则由右边程序框图输出的数值A组成一个数列{an}。
(1)求a1,a2,a3,a4和数列{an}的通项公式;
(2)若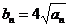 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。
19. 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1中点。
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1中点。
(1)求证:平面B1FC1//平面ADE;
(2)试在棱DC上求一点M,使D1 M平面ADE
M平面ADE
18.一个袋子中有红、白、蓝三种颜色的球共24个,除颜色外完全相同,已知蓝色球3个。若从袋子中随机取出1个球,取到红色球的概率是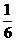 。
。
(1)求红色球的个数;
(2)若将这三种颜色的球分别进行编号,并将1号红色球,1号白色球,2号蓝色球和3号蓝色球这四个球装入另一个袋子中,甲乙两人先后从这个袋子中各取一个球(甲先取,取出的球不放回),求甲取出的球的编号比乙的大的概率。
17.已知A,B,C是 ABC的内角,a,b,c分别是其对边长,向量
ABC的内角,a,b,c分别是其对边长,向量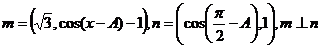 。
。
(1)求角A的大小;
(2)若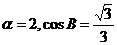 ,求b的长。
,求b的长。
16. 如图是函数f(x)=Asin(
如图是函数f(x)=Asin(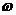 x+
x+ )(A>0,
)(A>0,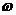 >0,
>0,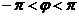 ),x
),x R的部分图象,则下列命题中,正确命题的序号为
R的部分图象,则下列命题中,正确命题的序号为
①函数f(x)的最小正周期为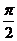 ;
;
②函数f(x)的振幅为2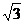 ;
;
③函数f(x)的一条对称轴方程为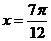 ;
;
④函数f(x)的单调递增区间为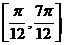 ;
;
⑤函数的解析式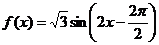 。
。
15.周长为定值的扇形OAB,当其面积最大时,向其内任意掷一点,则点落在 OAB内的概率
OAB内的概率
是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com