
20.(本题满分12分)已知过点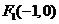 且斜率为1的直线
且斜率为1的直线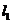 与直线
与直线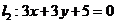
交于点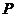 .
.
(1)求以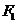 、
、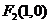 为焦点且过点
为焦点且过点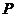 的椭圆
的椭圆 的方程;
的方程;
(2)设 点
点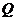 是椭圆
是椭圆 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在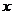 轴上是否存在两定点
轴上是否存在两定点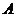 、
、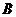 使
使
得直线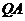 、
、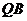 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点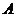 、
、
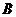 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
19. (本题满分12分)如图,直四棱柱
(本题满分12分)如图,直四棱柱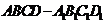
 中,
中,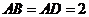 ,
,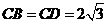 ,
,

 ,
,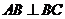 ,
, 与
与 交于点
交于点 .
.
(1)求证:
(2)求二面角
 的大小;
的大小;
(3)求异面直线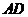 与
与 所成角的余弦值.
所成角的余弦值.
18.(本题满分13分)已知函数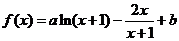 的图像与直线
的图像与直线 相
相
切于点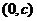
求(1)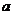 的值 (2)函数
的值 (2)函数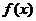 的单调区间和极小值
的单调区间和极小值
17.(本题满分13分)在一个不透明的盒子中,放有标号分别为1,2,3的三个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为 ,记
,记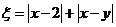 .
.
(1)求随机变量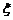 的最大值,并求事件“
的最大值,并求事件“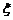 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量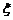 的分布列和数学期望.
的分布列和数学期望.
16.(本题满分13分)在
 中,
中,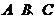 的对边分别为
的对边分别为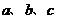 ,且
,且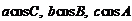
成等差数列.
(1)求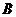 的值;
的值;
(2)求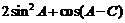 的范围.
的范围.
15.不等式 的解集是
.
的解集是
.
14. 设 满足约束条件
满足约束条件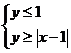 ,则
,则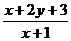 的取值范围是_________________.
的取值范围是_________________.
13. 过点
过点 且与抛物线
且与抛物线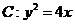 仅有一个公共点的直线方程是
.
仅有一个公共点的直线方程是
.
12.随机变量 ,如果
,如果 ,则
,则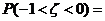 _____________.
_____________.
11.将函数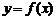 的图象沿向量
的图象沿向量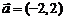 平移后,得到函数
平移后,得到函数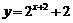 的图象,则函数
的图象,则函数
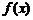 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com