
2. wanted
A. walked B. watched C. decided D. opened
第一节 语音知识(共5小题;每小题1分,满分5分)
从A、B、C、D四个选项中,找出其划线部分与所给单词的划线部分读音相同的选项,并在答题卡上将该项涂黑。
1. mirror
A. prize B. title C. village D. pile
22.(本小题满分12分)
已知函数 图像上点
图像上点 处的切线方程为与直线
处的切线方程为与直线 平行(其中
平行(其中 ),
),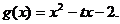
(I)求函数 的解析式;
的解析式;
(II)求函数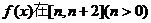 上的最小值;
上的最小值;
(III)对一切 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
21.(本小题满分12分)
已知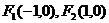 是椭圆
是椭圆 的两个焦点,点G与F2关于直线
的两个焦点,点G与F2关于直线 对称,且GF1与l的交点P在椭圆上.
对称,且GF1与l的交点P在椭圆上.
(I)求椭圆方程;
(II)若P、 是椭圆上的不同三点,直线PM、PN的倾斜角互补,问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
是椭圆上的不同三点,直线PM、PN的倾斜角互补,问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
20.(本小题满分12分)
已知数列 的首项
的首项 ,其前n项和为
,其前n项和为 ,当
,当 时,满足
时,满足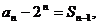
又
(I)证明:数列 是等差数列;
是等差数列;
(II)求数列 的前n项和
的前n项和
19.(本小题满分12分)
某校选派4人参加上级组织的数学竞赛,现从甲、乙两个竞赛班各选派2人.设甲、乙两班选派的人员获奖概率分别为 且4位选手是否获奖互不影响.
且4位选手是否获奖互不影响.
(I)求甲、乙两班各有1人获奖的概率;
(II)求该校获奖人数 的分布列与期望.
的分布列与期望.
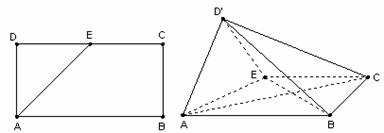
18.(本小题满分12分)
如图,在矩形 中,
中, ,
, ,
,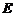 是
是 的中点,以
的中点,以 为折痕将
为折痕将 向上折起,使
向上折起,使
为 ,且平面
,且平面 平面
平面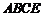
(Ⅰ)求证: ;
;
 (Ⅱ)求二面角
(Ⅱ)求二面角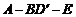 的大小
的大小
17. (本小题满分10分)
设函数f(x)=cos(2x+ )+sin
)+sin x.
x.
(1)求函数f(x)的最大值和最小正周期.
(2)设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=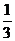 ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
16.在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数 z=x+ay取得最小值的最优解有无数个,则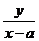 的最大值是__________.
的最大值是__________.
|
15、设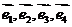 是平面内的四个单位向量,其中
是平面内的四个单位向量,其中 与
与 的夹角为
的夹角为 ,对这个平面内的任一个向量
,对这个平面内的任一个向量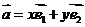 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量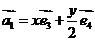 ,设向量
,设向量 ,则经过一次“斜二测变换”得到向量
,则经过一次“斜二测变换”得到向量 的模
的模 是______ _____.
是______ _____.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com