
24.(本小题满分10分)选修4-5:不等式选讲
已知函数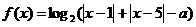
(Ⅰ)当 =2时,求函数
=2时,求函数 的最小值;
的最小值;
(Ⅱ)当函数 的定义域为
的定义域为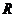 时,求实数
时,求实数 的取值范围。
的取值范围。
命题人:弓棚高中 于铁
23.(本小题满分10分)选修4-4:坐标系与参数方程选讲
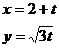
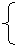 已知直线
已知直线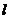 的参数方程为:
(t 为参数),曲线C的极坐标方程为:
的参数方程为:
(t 为参数),曲线C的极坐标方程为:
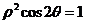
(1)求曲线C的普通方程;
(2)求直线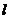 被曲线C截得的弦长
被曲线C截得的弦长
22.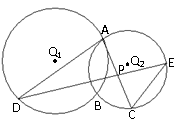 (本小题满分10分)选修4-1:几何证明选讲如图所示,⊙
(本小题满分10分)选修4-1:几何证明选讲如图所示,⊙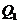 与⊙
与⊙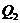 相交于
相交于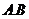 两点,过点
两点,过点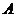 作⊙
作⊙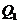 的切线交⊙
的切线交⊙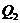 于点
于点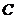 ,过点
,过点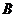 作两圆的割线,分别交⊙
作两圆的割线,分别交⊙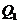 、⊙
、⊙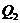 于点
于点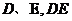 与
与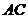 相交于点
相交于点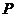
(Ⅰ)求证: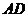 ∥
∥
(Ⅱ)若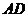 是⊙
是⊙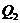 的切线,
的切线,
且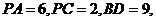 求
求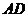 的长
的长
21.(理)(本小题满分12分)
已知函数 是奇函数,且满足
是奇函数,且满足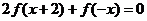 ,当
,当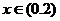 时,
时,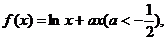 当
当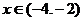 时,
时, 的最大值为
的最大值为
(1)求实数 的值;
的值;
(2)设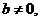 函数
函数 若对任意的
若对任意的 ,总存在
,总存在 ,使
,使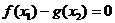 ,求实数
,求实数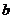 的取值范围。
的取值范围。
(文)(本小题满分12分)
已知椭圆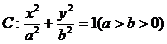 的离心率
的离心率 ,点
,点 为椭圆的右焦点,点
为椭圆的右焦点,点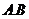 分别为椭圆的左.右顶点,点
分别为椭圆的左.右顶点,点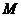 为椭圆的上顶点,且满足
为椭圆的上顶点,且满足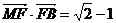
 (1)求椭圆
(1)求椭圆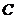 的方程;
的方程;
(2)是否存在直线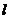 ,当直线
,当直线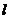 交椭圆于
交椭圆于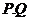 两点时,
两点时,
使点 恰为
恰为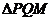 的垂心,若存在,求出直线
的垂心,若存在,求出直线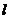 的
的
方程;若不存在,请说明理由。
请考生在22.23.24三题中任选一题作答,如果多做,则按
所做的第一题记分。
20.(理)(本小题满分12分)
已知抛物线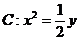 和定点
和定点 为抛物线
为抛物线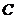 上的两个动点,且直线
上的两个动点,且直线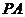 和
和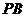 的斜率为非零的互为相反数。
的斜率为非零的互为相反数。
(1)求证:直线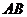 的斜率是定值;
的斜率是定值;
(2)若抛物线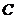 在
在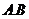 两点处的切线相交于点
两点处的切线相交于点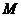 ,求
,求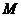 的轨迹方程;
的轨迹方程;
(3)若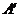 与
与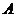 关于
关于 轴成轴对称,求直线
轴成轴对称,求直线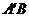 与
与 轴交点
轴交点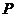 的纵坐标的取值范围。
的纵坐标的取值范围。
(文)(本小题满分12分)
已知函数
(1)求 的单调区间
的单调区间
(2)若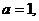 且
且 ,函数
,函数 ,若对任意的
,若对任意的 ,总存在
,总存在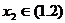 ,使
,使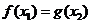 ,求实数
,求实数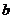 的取值范围。
的取值范围。
19.(理)(本小题满分12分)
为了让学生更多的了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竟赛活动,现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
|
序号 |
分组(分数段) |
频数(人数) |
频率 |
|
1 |
[60,70) |
① |
0.16 |
|
2 |
[70,80) |
22 |
② |
|
3 |
[80,90) |
14 |
0.28 |
|
4 |
[90,100] |
③ |
④ |
|
合计 |
50 |
1 |
(1)填空频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:为每位参加决赛的选手准备4道判断题,选手对其依次口答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对1道,则获得二等奖。
某同学进入决赛,每道题答对的概率p的值恰好与频率分布表中不少于80分的频率值相同。
(i)求该同学恰好答满4道题而获得一等奖的概率;
(ii)设该同学决赛中答题个数为X,求X的分布列及X的数学期望。
(文)(本小题满分12分)
某网站就网站就观众对2010春晚小品类节目的喜爱程度进行网上调查,其中持各种态度的人数如下表:
|
喜爱程度 |
喜欢 |
一般 |
不喜欢 |
|
人数 |
560 |
240 |
200 |
(1) 现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为n的样本,已知从不喜欢小品的观众中抽取的人数为5人,则n值为多少?
(2) 在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名为女性,现将抽取到的5名不喜欢小品的观众看成一个总体,从中任选两名观众,求至少有一名为女性观众的概率。
18.(理)(本小题满分12分)
如图所示,在三棱柱 中,
中,
侧面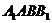 和
和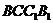 是两个全等的正方形,
是两个全等的正方形,
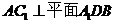 ,
,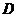 为
为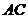 的中点。
的中点。
(1)求证:平面 平面
平面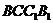 ;
;
(2)求证: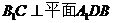
(3)设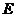 是
是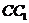 上一点,试确定点
上一点,试确定点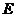 的位置,使平面
的位置,使平面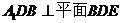 ,并说明理由。
,并说明理由。
(文)(本小题满分12分)
在正方体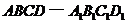 中,
中,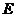 、
、 分别为棱
分别为棱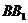 和
和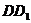 的中点。
的中点。
(1)求证: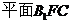 ∥平面
∥平面 ;
;
(2)试在棱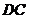 上取一点
上取一点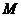 ,使
,使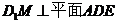 ;
;
(3)设正方体的棱长为1,求四面体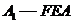 的体积。
的体积。
17.(本小题满分12分)
在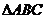 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足

(1)求角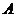 的大小
的大小
(2)若 ,试判断
,试判断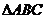 的形状,并说明理由。
的形状,并说明理由。
16.(理)已知真命题:若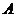 为⊙
为⊙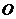 内一定点,
内一定点,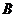 为⊙
为⊙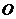 上一动点,
上一动点,
线段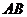 的垂直平分线交直线
的垂直平分线交直线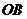 于点
于点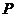 ,则点
,则点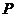 的轨迹是以
的轨迹是以
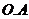 为焦点,
为焦点,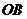 长为长轴长的椭圆。
长为长轴长的椭圆。
类比此命题,写出另一个真命题:若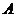 ⊙
⊙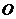 外一定点,
外一定点,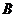 为⊙
为⊙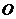 上一动点,线段
上一动点,线段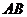 的垂直平分线交直线
的垂直平分线交直线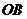 于点
于点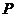 ,则点
,则点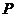 的轨迹是_________________
的轨迹是_________________
(文)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系 中,利用求动点轨迹方程的方法,可以求出过点
中,利用求动点轨迹方程的方法,可以求出过点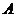 (-3,4),且其法向量为
(-3,4),且其法向量为 的直线方程为
的直线方程为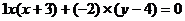 ,化简得
,化简得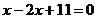 。类比上述方法,在空间坐标系
。类比上述方法,在空间坐标系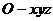 中,经过点
中,经过点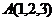 ,且其法向量为
,且其法向量为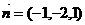 的平面方程为_______________________
的平面方程为_______________________
15.(理)右图是输出某个有限数列各项的程序框图,则该框图
所输出的最后一个数据是____________
(文)若函数 在其定义域内的一个子区间
在其定义域内的一个子区间
 内不是单调函数,则实数
内不是单调函数,则实数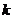 的取值范围是_______。
的取值范围是_______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com