
26.-Flight MU257 _______________ . I must be off now.
-Have a nice trip.
A. is being announced B. has announced
C. was announcing D. had been announced
25. When _______________ comes to saving energy, big changes start with small steps, like turning off the lights.
A. that B. this C. it D. one
24. Of the two cameras, I would prefer _______________ one, which is very easy for me to carry. K.s+5-u
A. a smaller B. the smallest C. a small D. the smaller
23. Mr Jones, a professor, ___________ for his excellent lectures, is popular with his students.
A. known B. knowing C. to be known D. having known
22.-Can you give some advice on what I said just now?
-Sorry. My mind______________.
A. is wandering B. was wandering
C. has wandered D. had wandered
第一节:语法和词汇知识(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
例:It is generally considered unwise to give a child ___________ he or she wants.
A. however B. whatever C. whichever D. whenever
答案是B。
21. Having __________ no-meat day would be a good way of encouraging ___________ low carbon life-style.
A. a; the B. a; a C. the; the D. the; a
20.(本小题满分13分)
设函数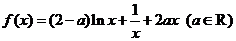 .
.
(1)当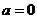 时,求
时,求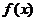 的极值;
的极值;
(2)当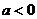 时,求
时,求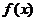 的单调区间;
的单调区间;
(3)若对任意 及
及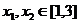 ,恒有
,恒有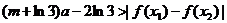 成立,
成立,
求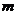 的取值范围.
的取值范围.
解:(1)依题意,知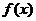 的定义域为
的定义域为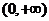 .
.
当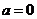 时,
时, ,
,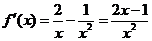 .
.
令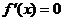 ,解得
,解得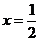 .
.
当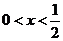 时,
时,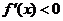 ;当
;当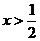 时,
时,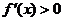 .
.
又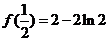 ,所以
,所以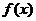 的极小值为
的极小值为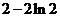 ,无极大值 .
,无极大值 .
(2)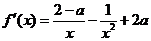
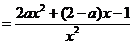
当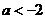 时,
时,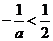 ,
,
令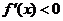 ,得
,得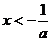 或
或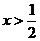 ,令
,令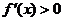 ,得
,得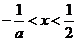 ;
;
当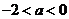 时,得
时,得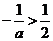 ,
,
令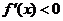 ,得
,得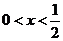 或
或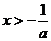 ,令
,令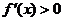 ,得
,得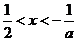 ;
;
当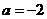 时,
时,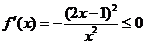 .
.
综上所述,当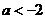 时,
时,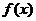 的递减区间为
的递减区间为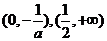 ;递增区间为
;递增区间为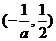 .
.
当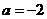 时,
时,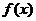 在
在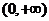 单调递减.
单调递减.
当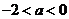 时,
时,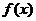 的递减区间为
的递减区间为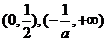 ;递增区间为
;递增区间为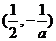 .
.
(3)由(2)可知,当 时,
时,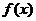 在
在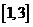 单调递减.
单调递减.
当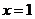 时,
时,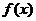 取最大值;当
取最大值;当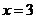 时,
时,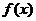 取最小值.
取最小值.
所以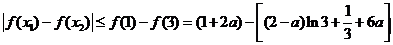
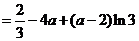 .
.
因为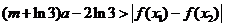 恒成立,
恒成立,
所以 ,整理得
,整理得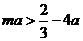 .
.
又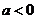 所以
所以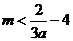 ,
,
又因为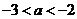 ,得
,得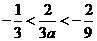 ,
,
所以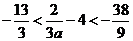 ,所以
,所以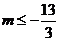 .
.
19.(本小题满分13分)在数列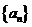 中,
中, ,
,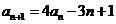 ,
,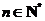 .
.
(1)证明数列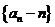 是等比数列;
是等比数列;
(2)求数列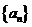 的前
的前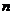 项和
项和 ;
;
(3)证明不等式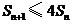 ,对任意
,对任意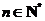 皆成立.
皆成立.
[解析](1)证明:由题设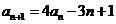 ,得
,得
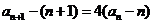 ,
,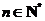 .
.
又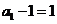 ,所以数列
,所以数列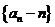 是首项为
是首项为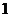 ,且公比为
,且公比为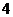 的等比数列.
的等比数列.
(2)解:由(1)可知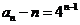 ,于是数列
,于是数列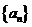 的通项公式为
的通项公式为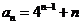 .
.
所以数列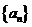 的前
的前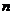 项和
项和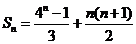 .
.
(3)证明:对任意的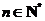 ,
,
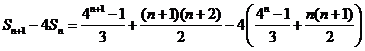
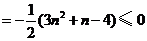 .
.
所以不等式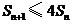 ,对任意
,对任意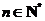 皆成立.
皆成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com