
8.(2003年普通高等学校招生全国统一考试(上海理17))
已知复数z1=cosθ-i,z2=sinθ+i,求|z1·z2|的最大值和最小值.
7.设z1,z2是两个虚数,且z1+z2=-3,|z1|+|z2|=4.若θ1=argz1,θ2=argz2,求cos(θ1-θ2)的最大值.
6、若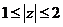 ,求
,求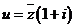 所对应的点A的集合表示的图形,并求其面积.
所对应的点A的集合表示的图形,并求其面积.
5、设A,B,C三点对应的复数分别为z ,z
,z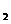 ,z
,z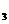 满足
满足

(1)证明:△ABC是内接于单位圆的正三角形;
(2)求S△ABC;
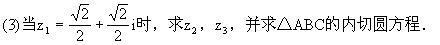
4、已知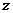 是虚数,
是虚数,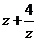 是实数。
是实数。
(1)求z对应复平面内动点A的轨迹;
(2)设u=3iz+1,求u对应复平面内动点B的轨迹;
(3)设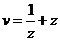 ,求
,求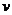 对应复平面内动点C的轨迹。
对应复平面内动点C的轨迹。
3、在复平面上绘出下列图形:
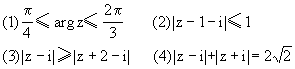
2、方程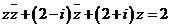 的图形是
[ ]
的图形是
[ ]
A.圆 B.椭圆 C.双曲线 D.直线
1、下列命题中正确的是 [ ]
A.方程|z+5|
 |z
|z 5i|
5i| =8的图形是双曲线
=8的图形是双曲线
B.方程|z+5| =8的图形是双曲线
=8的图形是双曲线
C.方程|z+5i| |z
|z 5i|=8的图形是双曲线的两支
5i|=8的图形是双曲线的两支
D.方程|z+5i| |z
|z 5i|=8的图形是双曲线靠近焦点F(0,5)的一支
5i|=8的图形是双曲线靠近焦点F(0,5)的一支
(二)范例分析
Ⅰ.2004年高考数学题选
1.(2004高考数学试题(浙江卷,6))已知复数z1=3+4i,
z2=t+i, 且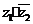 是实数,则实数t=( )
是实数,则实数t=( )
A.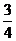 B.
B.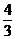 C.-
C.-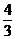 D.-
D.-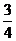
2.(2004年北京春季卷,2)当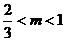 时,复数
时,复数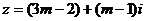 在复平面上对应的点位于
( )
在复平面上对应的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2004年北京卷,2)满足条件的复数在复平面上对应点的轨迹是( C )
A.一条直线 B.两条直线 C.圆 D.椭圆
Ⅱ.主要的思想方法和典型例题分析:
1.化归思想
复数的代数、几何、向量及三角表示,把复数与实数、三角、平面几何和解析几何有机地联系在一起,这就保证了可将复数问题化归为实数、三角、几何问题。反之亦然。这种化归的思想方法应贯穿复数的始终。
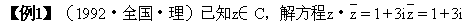
[分析]这是解答题,由于出现了复数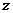 和
和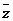 ,宜统一形式,正面求解。
,宜统一形式,正面求解。
解法一、设z=x+yi(x,y∈R),原方程即为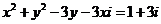
用复数相等的定义得:
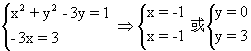
∴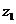 =
= 1,
1,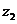 =
= 1+3i.
1+3i.
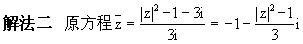

两边取模,得: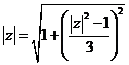
整理得 
解得  或
或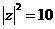
代入①式得原方程的解是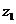 =
=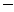 1,
1,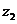 =
=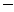 1+3i.
1+3i.
[例2](1993·全国·理)设复数z=cosθ+isinθ(0<

[解]∵z=cosθ+isinθ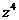 =cos4θ+isin4θ
=cos4θ+isin4θ
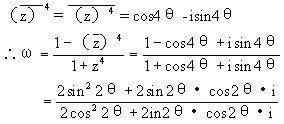
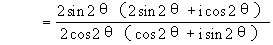
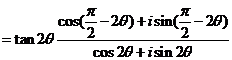
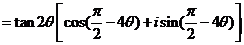
即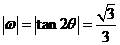 ,又∵0<θ<π,当
,又∵0<θ<π,当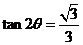 时,
时,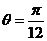 或
或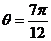
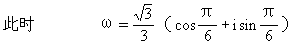
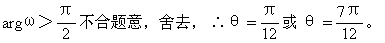
[说明]此题转化为三角问题来研究,自然、方便。
[例3]设a,b,x,y∈R+,且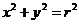 (r>0),
(r>0),
求证: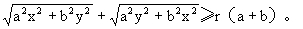
分析令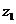 =ax+byi,
=ax+byi,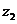 ==bx+ayi(a,b,x,y∈R+),则问题化归为证明:
==bx+ayi(a,b,x,y∈R+),则问题化归为证明:
|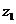 |+|
|+|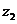 |≥r(a+b)。
|≥r(a+b)。
证明设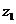 =ax+byi,
=ax+byi,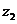 =bx+ayi(a,b,x,y∈R+),则
=bx+ayi(a,b,x,y∈R+),则
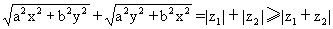
=|(a+b)x+(a+b)yi|=|(a+b)(x+yi)|=(a+b)·r。
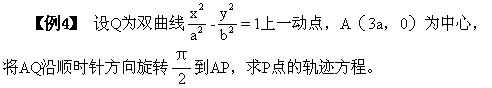

解如图所示,设点Q,P,A所对应的复数为:
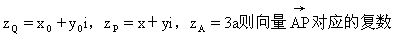

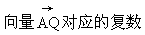
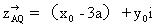

即(x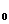
 3a+y
3a+y i)·(
i)·( i)=(x
i)=(x 3a+yi)
3a+yi)
由复数相等的定义得

而点(x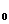 ,y
,y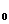 )在双曲线上,可知点P的轨迹方程为
)在双曲线上,可知点P的轨迹方程为

[说明]将复数问题化归为实数、三角、几何问题顺理成章,而将实数、三角、几何问题化归为复数问题,就要有较强的联想能力和跳跃性思维能力,善于根据题设构造恰到好处的复数,可使问题迎刃而解。
2.分类讨论思想
分类讨论是一种重要的解题策略和方法。在复数中它能使复杂的问题简单化,从而化整为零,各个击破。高考复数考题中经常用到这种分类讨论思想方法。
[例5](1990·全国·理)设a≥0,在复数集C中解方程z +2|z|=a。
+2|z|=a。
分析一般的思路是设z=x+yi(x,y∈R),或z=r(cosθ+isinθ),若由z +2|z|=a转化为z
+2|z|=a转化为z =a
=a 2|z|,则z
2|z|,则z ∈R。从而z为实数或为纯虚数,这样再分别求解就方便了。
∈R。从而z为实数或为纯虚数,这样再分别求解就方便了。
总之,是一个需要讨论的问题。
[解]解法一∵z =a
=a 2|z|∈R,∴z为实数或纯虚数。
2|z|∈R,∴z为实数或纯虚数。
∴问题可分为两种情况:
(1)若z∈R,则原方程即为|z| +2|z|
+2|z| a=0,
a=0,
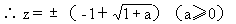
(2)若z为纯虚数,设z=yi(y∈R且y≠0),则原方程即为|y|
 2|y|+a=0
2|y|+a=0
当a=0时,|y|=2即z=±2i。
当0<a≤1时,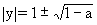
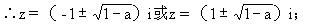
当a>1时,方程无实数解,即此时原方程无纯虚数解。
综上所述,原方程:
当a=0时,解为z=0或z=±2i
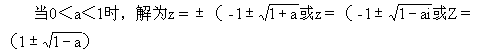
解法二设z=x+yi,x,y∈R,将原方程转化为
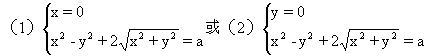
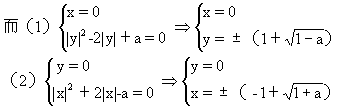
3.数形结合思想
数与形是数学主要研究内容,两者之间有着紧密的联系和互相渗透、互相转化的广阔前景,复平面的有关试题正是它的具体表现。运用数形结合思想与方法解题是高考考查的热点之一,应引起注意。
[例6]已知|z|=1,且z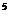 +z=1,求z。
+z=1,求z。
[解]由z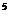 +z=1联想复数加法的几何性质,不难发现z,z
+z=1联想复数加法的几何性质,不难发现z,z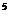 ,1所对应的三点A,B,C及原点O构成平行四边形的四个顶点,如图所示,
,1所对应的三点A,B,C及原点O构成平行四边形的四个顶点,如图所示,
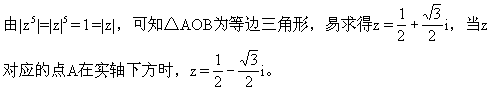
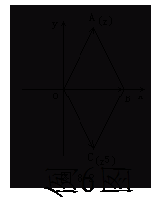
[说明]这样巧妙地运用联想思维,以数构形,以形思数,提炼和强化数形结合的思想方法,有利于培养学生思维的深刻性。
[例7]复平面内点A对应复数z,点B对应复数为,O为原点,△AOB是面积为的直角三角形,argz∈(0,),求复数z的值.
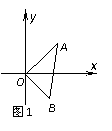 [分析]哪一个角为直角,不清楚,需要讨论.
[分析]哪一个角为直角,不清楚,需要讨论.
[解]因|OA|=|z|>||=|OB|,故∠A不可能是直角,因而可能∠AOB=90º或∠ABO=90º.
 若∠AOB=90º,示意图如图1所示.因z与所对应的点关于实轴对称,故argz=45º,
若∠AOB=90º,示意图如图1所示.因z与所对应的点关于实轴对称,故argz=45º,
S△AOB=|OA|·|OB|=|z|·||=|z|2=.于是,|z|=2,
从而,z=2(cos45º+isin45º)=+i.
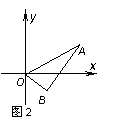
若∠ABO=90º,示意图如图2所示.因z与所对应的点关于实轴对称,且∠AOB<90º,故argz=θ<45º.
令z=r(cosθ+isinθ),则
cos2θ==,sin2θ=,S△AOB=|OA|·|OB|·sin2θ
=r·r·=r2=.
于是,r=. 又cosθ==,
sinθ==, 故z=(+i)=2+i.
综上所述,z=+i或z=2+i.
[说明]①解题关键点:正确地对直角的情况进行分类讨论,正确地理解复数的几何意义,作出满足条件的示意图.
②解题规律:复数的几何意义来源于复数z=a+bi(a、b∈R)与复平面上的点(a,b)之间的一一对应,它沟通了复数与解析几何之间的联系,是数形结合思想的典型表示.
③解题技巧:复数z与它的共轭复数在复平面内对应的向量关于实轴对称.
④这样巧妙地以形译数,数形结合,不需要计算就解决了问题,充分显示了数形结合的思想方法在解题中的作用。
4.集合对应思想
[例8]如图所示,在复平面内有三点P ,P
,P ,P
,P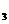 对应的复数
对应的复数
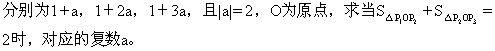
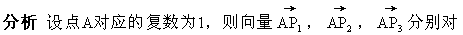
应的复数为a,2a,3a,且它们有相同的辐角主值θ(如图所示),即A,P ,P
,P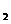 ,P
,P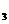 共线。
共线。
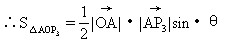
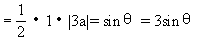
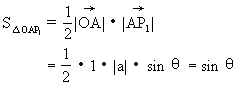
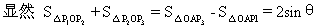
从而2sinθ=2
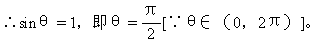
因此有a=±2i。
5.整体处理思想
解复数问题中,学生往往不加分析地用复数的代数形式或三角形式解题。这样常常给解题带来繁琐的运算,导致解题思路受阻。因此在复数学习中,有必要提炼和强化整体处理的思想方法,居高临下地把握问题的全局,完善认识结构,获得解题的捷径,从而提高解题的灵活性及变通性。
[例9]已知z=2 i,求z
i,求z
 3z
3z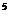 +z
+z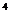 +5z
+5z +2的值。
+2的值。
[分析]如果直接代入,显然比较困难,将z用三角式表示也有一定的难度。从整体角度思考,可将条件转化为(z 2)
2) =(
=( i)
i) =
= 1,即z
1,即z
 4z+4=
4z+4= 1,即z
1,即z
 4z+5=0,再将结论转化为z
4z+5=0,再将结论转化为z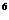
 3z
3z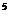 +z
+z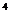 +5z
+5z +2=(z
+2=(z
 4z+5)(z
4z+5)(z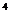 +z
+z )+2,然后代入就不困难了。
)+2,然后代入就不困难了。
[解]∵z=2 i,∴(z
i,∴(z 2)
2) =(
=( i)
i) =
= 1
1
即z
 4z+5=0
4z+5=0
∴z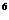
 3z
3z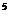 +z
+z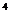 +5z
+5z +2=(z
+2=(z
 4z+5)(z
4z+5)(z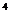 +z
+z )+2=2。
)+2=2。
[例10]已知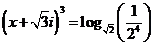 ,求
,求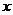 。
。
[解]解由条件得
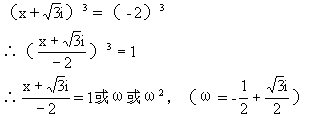
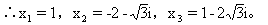
[说明]把题中一些组合式子视作一个“整体”,并把这个“整体”直接代入另一个式子,可避免由局部运算带来的麻烦。
[例11]复平面上动点z 的轨迹方程为:|z
的轨迹方程为:|z
 z
z |=|z
|=|z |,z
|,z ≠0,另一动点z满足z
≠0,另一动点z满足z ·z=
·z= 1,求点z的轨迹。
1,求点z的轨迹。
解由|z
 z
z |=|z
|=|z |,知点z
|,知点z 的轨迹为连结原点O和定点z
的轨迹为连结原点O和定点z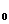 的线段的垂直平分线。
的线段的垂直平分线。
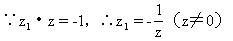
将此式整体代入点z1的方程,得
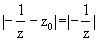



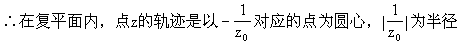
的圆(除去原点)。
[例12]设z∈c,a≥0,解方程z|z|+az+i=0。

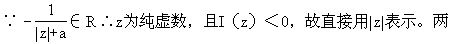
边取模,得
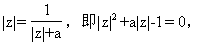
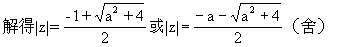
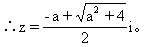
[说明]解复数方程,可通过整体取模,化为实数方程求解。
综上所述,解答复数问题,应注意从整体上去观察分析题设的结构特征,挖掘问题潜在的特殊性和简单性,充分利用复数的有关概念、共轭复数与模的性质、复数的几何意义以及一些变形技巧,对问题进行整体化处理,可进一步提高灵活、综合应用知识的能力。
6.有关最值问题的多角度思考
[例13]复数z满足条件|z|=1,求|2z
 z+1|的最大值和最小值。
z+1|的最大值和最小值。
解法一|z|=1,∴z=cosθ+isinθ
∴|2z
 z+1|=|2(cosθ+isinθ)
z+1|=|2(cosθ+isinθ)
 (cosθ+isinθ)+1|
(cosθ+isinθ)+1|
=|(2cos2θ cosθ+1)+(2sin2θ
cosθ+1)+(2sin2θ sinθ)i|
sinθ)i|
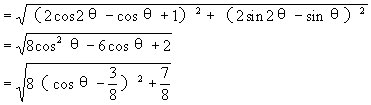
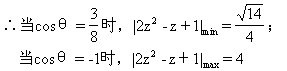
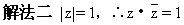
∴|2z
 z+1|
z+1| =|2z
=|2z
 z+
z+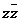 |
|
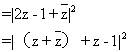
设z的实部为a,则 1≤a≤1
1≤a≤1
|2z
 z+1|=|2a+z
z+1|=|2a+z 1|
1|
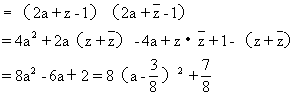
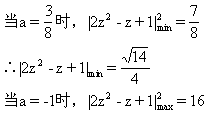 ,
,
∴|2z
 z+1|
z+1|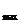 =4
=4
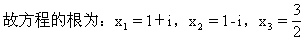
解法三:设ω=x+yi(x,y∈R),z=a+bi(a,b∈r)且a +b
+b =1,
=1,

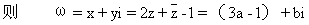
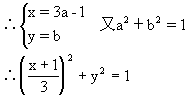
这说明ω对应的点是如图所示的椭圆,问题转化为求该椭圆上各点中与原点距离的最大值和最小值。
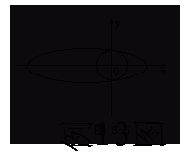
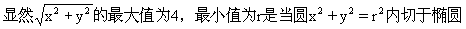
时的圆的半径。
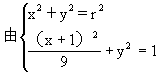
得8x
 2x+8
2x+8 9r
9r =0,
由相内切条件知Δ=0,
=0,
由相内切条件知Δ=0,
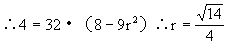
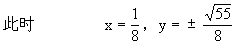

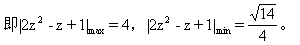
解法四由模不等式:
|2z
 z+1|≤2|z|
z+1|≤2|z| +|z|+1=4,等号成立的条件是2z
+|z|+1=4,等号成立的条件是2z ,
, z,1所对应的向量共线且同向,可知z是负实数,在|z|=1的条件下,z=-1
z,1所对应的向量共线且同向,可知z是负实数,在|z|=1的条件下,z=-1
∴当z= 1时|2z
1时|2z
 z+1|
z+1| =4。
=4。
但另一方面:|2z
 z+1|≥2|z|
z+1|≥2|z|
 |z|
|z| 1=0,这是显然成立的,可是这不能由此确定|2z
1=0,这是显然成立的,可是这不能由此确定|2z
 z+1|
z+1| =0,实际上等号成立的条件应为2z
=0,实际上等号成立的条件应为2z ,
, z,1表示的向量共线且异向,由2z
z,1表示的向量共线且异向,由2z 与1对应的向量共线且异向知z=±i,但是当z=±i时,2z
与1对应的向量共线且异向知z=±i,但是当z=±i时,2z 与
与 z不共线,这表明|2z
z不共线,这表明|2z
 z+1|的最小值不是0。
z+1|的最小值不是0。
以上这种求最小值的错误想法和解法是学生易犯的错误,此部分内容既为重点也为难点,应向学生强调说明,并举例,切记取等号的条件。
[例14]2001年普通高等学校招生全国统一考试(理18)
已知复数z1=i(1-i)3. (Ⅰ)求argz1及|z|; (Ⅱ)当复数z满足|z|=1,求|z-z1|的最大值.
[分析]本小题考查复数的基本性质和基本运算,以及分析问题和解决问题的能力.
[解](Ⅰ)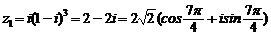
∴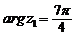 ,|z1|=
,|z1|=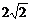 .
.
(Ⅱ)设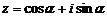 ,则
,则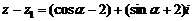
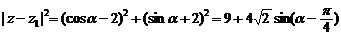 当
当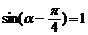 时,
时,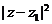 取得最大值
取得最大值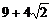 ,从而得到
,从而得到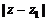 的最大值为
的最大值为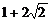 .
.
(一)主要知识:
1.共轭复数规律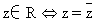 ,
, ;
;
2.复数的代数运算规律
(1)i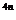 =1,i
=1,i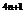 =i,i
=i,i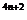 =
= 1,i
1,i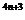 =
= i;
i;
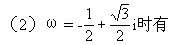
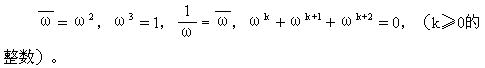
(3)i ·i
·i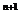 ·i
·i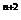 ·i
·i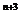 =
= 1,i
1,i +i
+i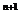 +i
+i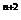 +i
+i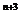 =0;
=0;
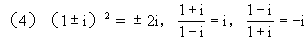 ;
;
3.辐角的运算规律
(1)Arg(z ·z
·z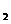 )=Argz
)=Argz +Argz
+Argz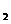
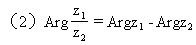
(3)Arg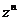 =nArgz(n∈N)
=nArgz(n∈N)

…,n 1。
1。
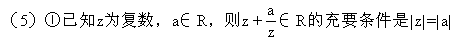
或z∈R。

要条件是|z|=|a|。
(6)z ·z
·z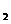 ≠0,则
≠0,则
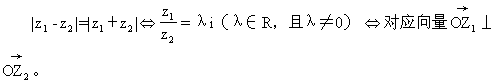
4.根的规律:复系数一元n次方程有且只有n个根,实系数一元n次方程的虚根成对共轭出现。
5.求最值时,除了代数、三角的常规方法外,还需注意几何法及不等式
||z |
| |z
|z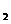 ||≤|z
||≤|z ±z
±z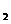 |≤|z
|≤|z |+|z
|+|z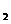 |的运用。
|的运用。
即|z ±z
±z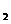 |≤|z
|≤|z |+|z
|+|z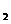 |等号成立的条件是:z
|等号成立的条件是:z ,z
,z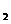 所对应的向量共线且同向。
所对应的向量共线且同向。
|z ±z
±z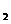 |≥|z
|≥|z |
| |z
|z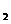 |等号成立的条件是:z
|等号成立的条件是:z ,z
,z 所对立的向量共线且异向。
所对立的向量共线且异向。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com