4、求经过点P(1，2)，且与A(2，3)、B(4，-5)两点的距离相等的直线l的方程.

3、已知三条直线相交于一点，求m的值.

2、若的交点在第　　　　 象限.

1、两条直线的夹角等于　　　　　 .

5、直线系方程：

(1)共点直线系：例：过点P(a,b)的直线系方程为x=a或y-b=k(x-a).

(2)平行直线系：例：和直线Ax+By+C=0平行的直线系方程为Ax+By+C₁=0.

(3)过两直线交点的直线系：

经过两条直线l₁:A₁x+B₁y+C₁=0和l₂:A₂x+B₂y+C₂=0的交点的直线系方程是：

A₁x+B₁y+C₁+λ(A₂x+B₂y+C₂)=0(不包括直线两条平行直线l₂).

基础练习：

4、点到直线的距离：

已知点P(x₀,y₀)和直线l:Ax+By+C=0，则点

P到直线l的距离为：.

(2)点P(x₀,y₀)到直线l:x=a的距离d=|x₀-a|；

到直线l:y=b的距离d=|y₀-b|.

两条平行直线l₁:Ax+By+C₁=0和l₂:Ax+By+C₂=0

之间的距离.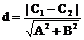

3、两条直线的交点：

(1)交点的求法：。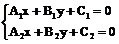

(2)根据方程组的解的情形讨论两条直线的位置关系：

若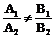，则两条直线相交，有且只有一个交点；

若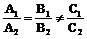，则两条直线平行，没有公共点；

若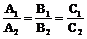，则两条直线重合，有无数个公共点。

2、两条直线所成的角：

(1)“到角”：两条直线l₁和l₂相交，我们把直线l₁依逆时针方向旋转到与

l₂重合时所转的角，叫做l_l到l₂的角，“到角”的取值范围是

(0°，180°)。

已知直线的方程分别是

l₁：y=k₁x+b₁,l₂：y=k₂x+b₂, l_l到l₂的角为，。

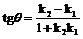(2)“夹角”：两条相交直线所成的锐角和直角就是两条直线所成的角。已知直线的方程分别是l₁：y=k₁x+b₁,l₂：y=k₂x+b₂, 它们的夹角为，。

1、两条直线的平行与垂直：

(1)平行：

设直线l₁和l₂的斜率为k₁和k₂，它们的方程分别是

l₁：y=k₁x+b₁,l₂：y=k₂x+b₂,则l₁∥l₂k₁=k₂.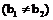

若两条平行直线中的一条直线的斜率不存在，

则另一条直线的斜率也不存在；反之亦然。

(2)垂直：

设直线l₁和l₂的斜率为k₁和k₂，

它们的方程分别是

l₁：y=k₁x+b₁,l₂：y=k₂x+b₂, 则。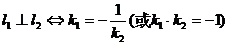

若两条互相垂直直线中的一条直线的斜率不存在或为零，则另一条直线的斜率必为零或不存在；反之亦然。

3、掌握点到直线的距离公式。

[知识内容]