11．已知f(x+2)＝f(x)(x∈R)，并且当x∈[－1,1]时，f(x)＝－x²+1，求当x∈[2k－1,2k+1](k∈Z)时、f(x)的解析式．

解：由f(x+2)＝f(x)，可推知f(x)是以2为周期的周期函数．当x∈[2k－1,2k+1]时，2k－1≤x≤2k+1，－1≤x－2k≤1.∴f(x－2k)＝－(x－2k)²+1.

又f(x)＝f(x－2)＝f(x－4)＝…＝f(x－2k)，

∴f(x)＝－(x－2k)²+1，x∈[2k－1,2k+1]，k∈Z.

10．函数f(x)＝.

(1)若f(x)的定义域为R，求实数a的取值范围；

(2)若f(x)的定义域为[－2,1]，求实数a的值．

解：(1)①若1－a²＝0，即a＝±1，

(ⅰ)若a＝1时，f(x)＝，定义域为R，符合题意；

(ⅱ)当a＝－1时，f(x)＝，定义域为[－1，+∞)，不合题意．

②若1－a²≠0，则g(x)＝(1－a²)x²+3(1－a)x+6为二次函数．

由题意知g(x)≥0对x∈R恒成立，

∴∴

∴－≤a<1.由①②可得－≤a≤1.

(2)由题意知，不等式(1－a²)x²+3(1－a)x+6≥0的解集为[－2,1]，显然1－a²≠0且－2,1是方程(1－a²)x²+3(1－a)x+6＝0的两个根．

∴∴∴a＝2.

9．有一个有进水管和出水管的容器，每单位时间进水量是一定的，设从某时刻开始，5分钟内只进水，不出水，在随后的15分钟内既进水，又出水，得到时间x与容器中的水量y之间关系如图．再随后，只放水不进水，水放完为止，则这段时间内(即x≥20)，y与x之间函数的函数关系是________．

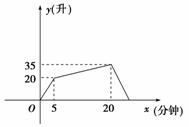
解析：设进水速度为a₁升/分钟，出水速度为a₂升/分钟，则由题意得，得，则y＝35－3(x－20)，得y＝－3x+95，又因为水放完为止，所以时间为x≤，又知x≥20，故解析式为y＝－3x+95(20≤x≤)．答案：y＝－3x+95(20≤x≤)

8．(2009年高考山东卷)定义在R上的函数f(x)满足f(x)＝则f(3)的值为________．

解析：∵f(3)＝f(2)－f(1)，又f(2)＝f(1)－f(0)，∴f(3)＝－f(0)，∵f(0)＝log₂4＝2，∴f(3)＝－2.答案：－2

7．(2009年高考天津卷改编)设函数f(x)＝，则不等式f(x)>f(1)的解集是________．

解析：由已知，函数先增后减再增，当x≥0，f(x)>f(1)＝3时，令f(x)＝3，

解得x＝1，x＝3.故f(x)>f(1)的解集为0≤x<1或x>3.

当x<0，x+6＝3时，x＝－3，故f(x)>f(1)＝3，解得－3<x<0或x>3.

综上，f(x)>f(1)的解集为{x|－3<x<1或x>3}．答案：{x|－3<x<1或x>3}

6．设函数f(x)＝log_ax(a＞0，a≠1)，函数g(x)＝－x²+bx+c，若f(2+)－f(+1)＝，g(x)的图象过点A(4，－5)及B(－2，－5)，则a＝__________，函数f[g(x)]的定义域为__________．

答案：2　 　(－1,3)

5．设函数f(x)＝，若f(－4)＝f(0)，f(－2)＝－2，则f(x)的解析式为f(x)＝________，关于x的方程f(x)＝x的解的个数为________个．

解析：由题意得

?，

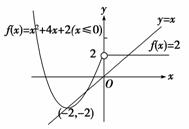
∴f(x)＝.

由数形结合得f(x)＝x的解的个数有3个．

答案：　3

4．设函数y＝f(x)满足f(x+1)＝f(x)+1，则函数y＝f(x)与y＝x图象交点的个数可能是________个．

解析：由f(x+1)＝f(x)+1可得f(1)＝f(0)+1，f(2)＝f(0)+2，f(3)＝f(0)+3，…本题中如果f(0)＝0，那么y＝f(x)和y＝x有无数个交点；若f(0)≠0，则y＝f(x)和y＝x有零个交点．答案：0或无数

3．定义在区间(－1,1)上的函数f(x)满足2f(x)－f(－x)＝lg(x+1)，则f(x)的解析式为________．

解析：∵对任意的x∈(－1,1)，有－x∈(－1,1)，

由2f(x)－f(－x)＝lg(x+1)，①

由2f(－x)－f(x)＝lg(－x+1)，②

①×2+②消去f(－x)，得3f(x)＝2lg(x+1)+lg(－x+1)，

∴f(x)＝lg(x+1)+lg(1－x)，(－1<x<1)．

答案：f(x)＝lg(x+1)+lg(1－x)，(－1<x<1)

2．(2010年山东枣庄模拟)函数f(x)＝则f(f(f()+5))＝_.

解析：∵－1≤≤2，∴f()+5＝－3+5＝2，∵－1≤2≤2，∴f(2)＝－3，

∴f(－3)＝(－2)×(－3)+1＝7.答案：7