
1.关于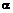 粒子散射实验,下列说法正确的是( )
粒子散射实验,下列说法正确的是( )
A.原子中的正电荷和几乎全部质量都集中在很小的区域范围内
B.实验结果支持了汤姆生的“枣糕模型”
C.依据该实验结果,卢瑟福提出了原子的核式结构模型
D.该实验结果表明了原子核不是构成物质的最小结构单元,原子核还可以再分
|
|
A.放射性元素的半衰期与温度无关
B.三种射线中,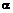 射线的电离本领最强,
射线的电离本领最强,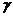 射线贯穿本领最强
射线贯穿本领最强
C.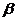 衰变说明原子核中有电子存在
衰变说明原子核中有电子存在
D.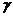 射线是放射性的原子核发生衰变时,原始核从高能级向低能级跃迁时产生的
射线是放射性的原子核发生衰变时,原始核从高能级向低能级跃迁时产生的
21.(本小题满分14分)
设数列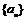 的前n项和为
的前n项和为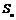 ,已知
,已知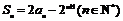 .
.
(1)求数列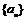 的通项公式;
的通项公式;
(2)令 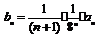 .用数学归纳法证明:
.用数学归纳法证明:
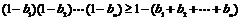 ;
;
(3)设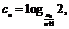 数列
数列 的前n项和为
的前n项和为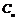 ,若存在整数m,使对任意
,若存在整数m,使对任意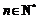 且
且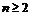 ,都有
,都有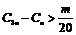 成立,求m的最大值.
成立,求m的最大值.
孝感高中2009-2010学年度下学期高二期末统一考试
20.(本小题满分13分)
已知函数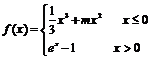
(1)讨论函数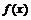 的极值情况;
的极值情况;
(2)设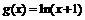 ,当
,当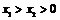 时,试比较
时,试比较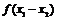 与
与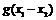 及
及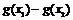 三者的大小;并说明理由.
三者的大小;并说明理由.
19.(本小题满分12分)
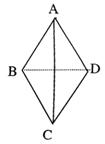 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为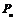 .求
.求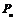 .
.
18.(本小题满分12分)
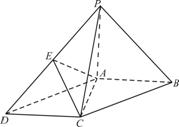 如图,在底面为平行四边形的四棱锥P-ABCD中,
如图,在底面为平行四边形的四棱锥P-ABCD中,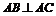 ,
,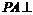 平面
平面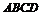 ,且
,且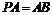 ,点E是PD的中点.
,点E是PD的中点.
(1)证明: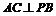 ;
;
(2)证明: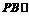 平面AEC;
平面AEC;
(3)求二面角E-AC-B的大小.
17.(本小题满分12分)
某单位选派甲、乙、丙三人组队参加“2010上海世博会知识竞赛”,甲、乙、丙三人在同时回答一道问题时,已知甲答对的概率是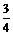 ,甲、丙两人都答错的概率是
,甲、丙两人都答错的概率是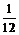 ,乙、丙两人都答对的概率是
,乙、丙两人都答对的概率是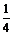 ,规定每队只要有一人答对此题则记该队答对此题.
,规定每队只要有一人答对此题则记该队答对此题.
(Ⅰ)求该单位代表队答对此题的概率;
(Ⅱ)此次竞赛规定每队都要回答10道必答题,每道题答对得20分,答错除该题不得分外还要倒扣去10分.若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其它题没有影响,求该单位代表队必答题得分的期望(精确到1分).
16.(本小题满分12分)
设函数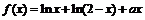 .
.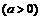 .
.
(1)当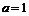 时,求
时,求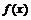 的单调区间;
的单调区间;
(2)若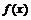 在
在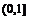 上的最大值为
上的最大值为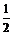 ,求
,求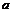 的值.
的值.
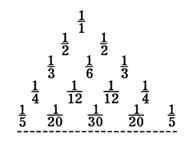
15.如右图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是
由整数的倒数组成的,第n行有n个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如
 ,…,则第10行第4个数(从左
,…,则第10行第4个数(从左
往右数)为 .
14.设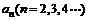 是
是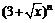 展开式中
展开式中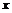 的一次项的系数,则
的一次项的系数,则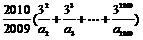 的值是
的值是
 .
.
13.设三棱锥3个侧面两两互相垂直,且侧棱长均为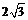 ,则其外接球的表面积为
.
,则其外接球的表面积为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com