
19.(本小题满分12分)
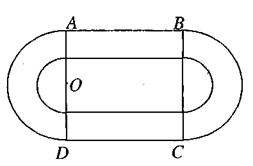
某学校要建造一个面积为10000平方米的运动场,如图,运动场是由一个矩形ABCD和分别以AD,BC为直径的两个半圆组成。跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮。已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元。
(I)设半圆的半径OA=r(米),试建立塑胶跑道面积S与r的函数关系S(r);
 (II)由于条件限制
(II)由于条件限制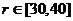 ,问当r为何值时,运动场造价最低?
,问当r为何值时,运动场造价最低?
18.(本小题满分12分)
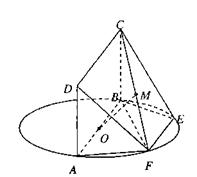
如图,AB为圆O的直径,点E、F在圆O上,且AB//EF,矩形ABCD所在的平面
和圆O所在的平面互相垂直,且AB=2,AD=EF=AF=1。
(I)求四棱锥F-ABCD的体积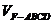 ;
;
(II)求证:平面AFC⊥CBF;
(II)在线段CF上是否存在一点M,使得OM//平面ADF,并说明理由。
17.(本小题满分12分)
设角A、B、C是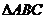 的三个内角,已知向量
的三个内角,已知向量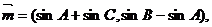
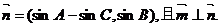
(I)求角C的大小;
(II)若向量 试求
试求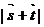 的取值范围。
的取值范围。
16.当实数x满足约束条件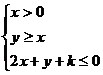 (其中k为小于
(其中k为小于
零的常数)时,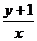 的最小值为2,则实数k的值
的最小值为2,则实数k的值
是 。
15.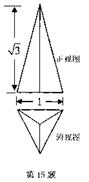 若正三棱锥的正视图与俯视图如右图所示(单位cm),
若正三棱锥的正视图与俯视图如右图所示(单位cm),
则它的侧视图的面积为 cm2。
14.已知点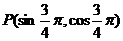 落在角
落在角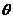 的终边上,且
的终边上,且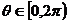 ,则
,则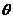 的值为
的值为
。
13.某大型超市销售的乳类商品有四种:纯奶、酸奶、婴幼儿奶粉、成人奶粉,且纯奶、酸奶、婴幼儿奶粉、成人奶粉分别有30种、10种、35种、25种不同的品牌,现采用分层抽样的方法从中抽取一个容量为n的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是7种,则n= 。
12.数列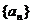 满足
满足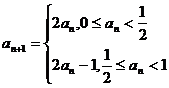 ,若
,若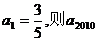 = ( )
= ( )
A.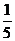 B.
B.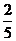 C.
C.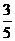 D.
D.
第Ⅱ卷(非选择题 共90分)
11.已知直线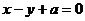 与圆
与圆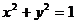 交于不同两点A、B,O为坐标原点,则
交于不同两点A、B,O为坐标原点,则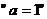 是“向量
是“向量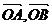 满足
满足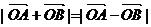 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.设点M(a,b)是曲线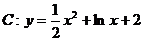 上的任意一点,直线
上的任意一点,直线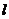 是曲线C在点M处的切线,那么直线
是曲线C在点M处的切线,那么直线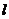 斜率的最小值为 ( )
斜率的最小值为 ( )
A.-2 B.0 C.2 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com